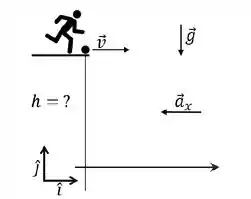
Um estudante chuta um rojão do alto de uma plataforma de altura acima do solo. O rojão é lançado com uma velocidade inicial horizontal de módulo . Entretanto, um forte vento que sopra paralelo ao solo faz com que o rojão tenha uma aceleração constante , sendo o módulo da componente horizontal da aceleração. Isso acaba por fazer com que o rojão caia no chão diretamente abaixo do estudante. Utilize o sistema de coordenadas indicado na figura e dê suas respostas em termos de , e .
a) Determine a altura da plataforma.
b) Determine o vetor velocidade do rojão imediatamente antes dele atingir o solo. Sua resposta deve ser dada em termos dos vetores unitários indicados na figura.
c) Qual é o alcance máximo, na horizontal, atingido pelo rojão em relação à plataforma?
Passo 1
Opa! Vamos lá!
Quando temos um movimento desse tipo (de lançamento) a gente analisa as duas direções separadamente.
Na direção x, temos:
Na direção y, temos:
Então, olha só, ambos tem aceleração cujo módulo é constante, então temos, um MUV em ambas direções.
Ok até aqui?
Vamos pra letra (a).
Passo 2
a) Determine a altura da plataforma.
A altura é o que? É uma posição, certo? E é uma posição na direção vertical. Então vamos usar a equação da posição em função do tempo, para a direção y:
O rojão parte da altura , então . A altura final dele é , pois ele vai chegar no chão.
Já substitui umas informações que falamos lá no passo 1.
Então beleza, temos que:
Eita...pra acharmos a altura, temos que achar o tempo . Mas que tempo é esse?
É o tempo correspondente a queda desde a altura até o chão. Então esse é o tempo de queda .
bora achar esse tempo de queda!
Pra isso, vamos analisar o movimento na direção horizontal.
Passo 3
No eixo x, temos um MUV. Então a equação da posição em função do tempo é:
O enunciado fala pra gente que o rojão cai no chão diretamente abaixo do estudante, ou seja:
Temos também que:
e
Substituindo isso tudo, temos:
Isolando o :
A solução (não nula) dessa equação é:
Show de bola! Esse é o tempo necessário para o rojão cair.
Agora, vamos substituir isso na nossa equação para :
resolvendo isso:
Uhuul!!
Vamos pra próxima!
Passo 4
b) Determine o vetor velocidade do rojão imediatamente antes dele atingir o solo. Sua resposta deve ser dada em termos dos vetores unitários indicados na figura.
O vetor velocidade é dado por:
Temos um MUV em ambas as direções, então a velocidade é dada por:
Como queremos o vetor velocidade imediatamente antes do rojão tocar o solo, temos que usar o tempo de queda para achar as componentes e .
Substituindo nossos dados, temos:
E para :
Então o vetor velocidade imediatamente antes do rojão tocar o solo é:
Tranquilo?
Passo 5
c) Qual é o alcance máximo, na horizontal, atingido pelo rojão em relação à plataforma?
O alcance é o que? É uma posição, certo? E na horizontal.
Então vamos usar a equação de Torricelli:
O alcance máximo ocorre quando o rojão não consegue ir mais pra frente (por isso que é máximo..kkk). E isso vai acontecer quando a velocidade em x for zero.
Então:
A posição inicial é zero. Então resolvendo isso, temos:
Esse é o alcance máximo!
Show?

Resposta
a)
b)
c)