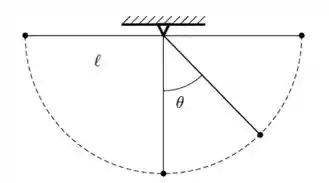
Uma pequena esfera de massa m é presa na extremidade de um fio ideal de comprimento ` que tem sua outra extremidade presa a um ponto no teto, formando um pêndulo, como indicado na figura. A esfera é solta de uma posição horizontal, passando a se movimentar pela trajetória como a indicada.
São feitas as seguintes observações sobre o movimento
do pêndulo:
I) Quando na posição mais baixa, a componente tangencial da aceleração possui seu valor máximo.
II) Quando a massa m passa pela posição mais baixa, temos que a tração feita pelo fio sobre a
massa é máxima.
III) A massa m descreve um movimento circular uniforme pois a resultante das forças é a centrípeta.
Quais das afirmações acima estão incorretas:
(a) I) e III)
(b) Apenas I)
(c) Apenas II)
(d) Apenas III)
(e) I) e II)
(f) II) e III)
Passo 1
Durante o movimento, temos 2 forças atuando: o peso e a tração.
Vamos analisar cada alternativa.
I) Quando na posição mais baixa, a componente tangencial da aceleração possui seu valor máximo.
Na posição mais baixa as forças vão estar assim:
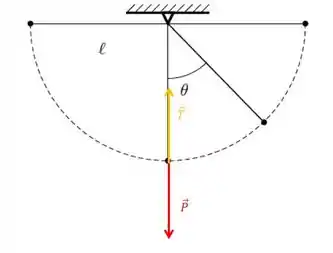
Então, vemos que, na posição mais baixa, não temos uma componente tangencial da aceleração. Aqui a aceleração está na forma de aceleração centrípeta.
Logo, nessa posição a aceleração tangencial é nula. Então essa é falsa.
Passo 2
II) Quando a massa m passa pela posição mais baixa, temos que a tração feita pelo fio sobre a
massa é máxima.
Ainda estamos na posição mais baixa. Nessa situação, temos a segunda lei de Newton assim:
Assim:
Em qualquer outra posição, teremos que a força na direção radial é:
Pois:
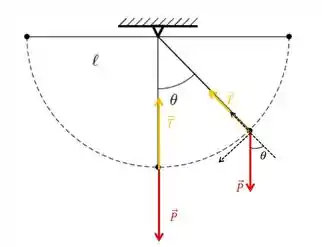
Então, na posição mais baixa é de fato quando o módulo da tração é máximo.
Passo 3
III) A massa m descreve um movimento circular uniforme pois a resultante das forças é a centrípeta.
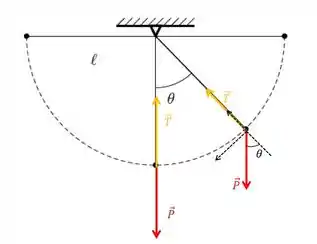
Olhando pra qualquer posição que não seja a mais baixa, vemos que existe uma componente da força peso não nula na direção tangencial.
Logo, existe uma força resultante na direção tangencial.
Essa também tá errada.
Resposta
Alternativa A.