P2 de Física 1 da UFRJ - 2013.2

Um sistema é constituído por duas partículas de mesma massa e uma barra fina homogênea sobre uma mesa horizontal sem atrito. As partículas estão em movimentos retilíneos uniformes com trajetórias paralelas e velocidades respectivas e . Elas colidem, simultaneamente, cada uma com uma extremidade da barra, que está em repouso e perpendicular às trajetórias, como indicado na figura. Após a colisão as partículas permanecem presas à barra e o sistema passa a girar com velocidade angular constante em torno do centro da barra.

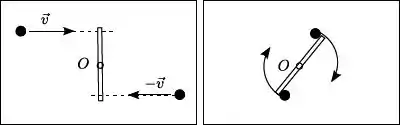
Sobre o momento linear do sistema, o seu momento angular relativo ao ponto e sua energia cinética podemos afirmar que

1. Conserva-se o momento linear mas não o angular;
2. Conservam-se os momentos linear e angular;
3. Conserva-se o momento angular mas não o linear;
4. Não se conservam os momentos linear e angular;
5. Não se conservam o momento linear e a energia cinética.

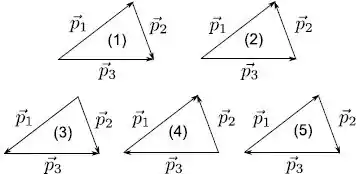
Uma granada encontra-se em repouso sobre uma mesa horizontal lisa (sem atrito) e explode em três fragmentos. Os fragmentos adquirem momentos lineares , e de módulos diferentes de zero, cuja direções formam ângulos diferentes entre si. O diagrama correto que representa a relação entre os momentos lineares deste fragmentos é

Uma partícula move-se com velocidade constante ao longo de uma reta paralela ao eixo que corta o em . Sejam , e os momentos angulares da partícula, relativos à origem , nos pontos , e , como indicados na figura. Os módulos dos momentos angulares são tais que

1. ;
2. ;
3. ;
4. ;
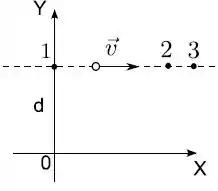
5. e ;

Uma barra fina e homogênea de massa e comprimento é liberada na posição horizontal a partir do repouso e gira em torno de um eixo horizontal fixo, perpendicular a ela e que passa por uma de suas extremidades. Sabendo que não há atrito entre a barra e o eixo e que o momento de inércia da barra relativo ao eixo é igual a , podemos afirmar que ao passar pela posição vertical a velocidade do centro de massa da barra é

1. ;
2. ;
3. ;
4. ;
5. ;

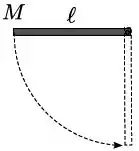
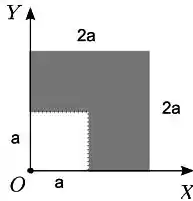
Uma chapa homogênea quadrada de lado tem um canto quadrado de lado retirado. A chapa restante está disposta no plano como indicado na figura. Em relação à origem , o vetor posição do centro de massa

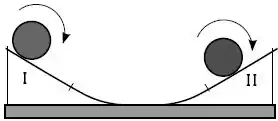
Considere uma esfera que rola sem deslizar sobre uma calha simétrica que tem dois trechos retilíneos, e , como mostrado na figura. Ela oscila descendo e subindo nos dois ramos da calha. No trecho a força de atrito é e no trecho , é . Considere que as únicas forças que atuam sobre a esfera sejam a força normal e a força de atrito exercidas pela calha, e seu peso.

Dentre os diagramas seguintes

O que melhor representa o sentido e a direção das forças de atrito e nos trechos e é

1. ;
2. ;
3. ;
4. ;
5. ;

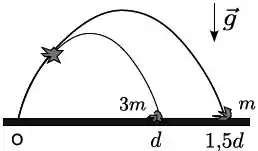
Um projétil é lançado de uma plataforma do ponto e num dado instante após ser lançado ele se fragmenta em dois pedações de massa e , que caem simultaneamente nas posições horizontais e respectivamente. Se o projétil não se fragmentasse o seu alcance seria,

1. ;
2. ;
3. ;
4. ;
5. ;

Uma chapa quadrada fina e homogênea de lado encontra-se sobre uma superfície horizontal sem atrito presa por um pino em um dos seus vértices. Num dado instante aplicam-se quatro forças horizontais e de mesma intensidade perpendiculares aos lados do quadrado como mostra a figura. O módulo do torque resultante em relação a é

1. ;
2. ;
3. ;
4. ;
5. ;

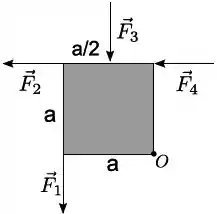
Um disco homogêneo de raio e massa rola sem deslizar sobre uma superfície horizontal com velocidade angular constante. O momento de inércia deste disco em relação ao eixo que passa pelo seu centro de massa, perpendicularmente ao disco, é igual a . A energia cinética desse disco é

1. ;
2. ;
3. ;
4. ;
5. ;

Dois alteres e mostrados na figura giram em torno de seus respectivos centros de massa em torno de um eixo fixo e perpendicular ao seu comprimento. O haltere gira com velocidade angular constante e o haltere com velocidade angular constante . No haltere as massas de suas extremidades são iguais a e no haltere . Os módulos de seus momentos angulares e em relação aos respectivos centros de massa e as suas energias cinéticas e cinéticas são relacionados respectivamente como

1. e
2. e
3. e
4. e
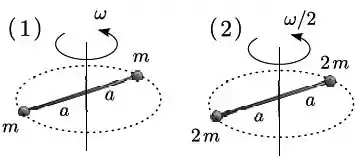
5. e

Dois blocos e de massas e , respectivamente, encontraram-se sobre uma superfície horizontal lisa. O bloco desloca-se com velocidade horizontal constante, enquanto o bloco encontra-se em repouso. Após a colisão os blocos separam-se e observa-se que o bloco de massa recua movendo-se com velocidade de módulo na mesma direção do seu deslocamento inicial, como mostra a figura.

1. Determine , o módulo da velocidade do bloco após a colisão.
2. Calcule o módulo da velocidade do centro de massa dos blocos antes e depois da colisão.
3. Determine a variação da energia cinética do sistema no processo da colisão.

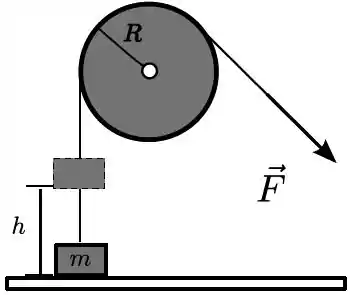
Um disco de raio e massa encontra-se fixado a uma parede vertical em um pino que passa pelo seu centro. Um cabo de massa desprezível passando pela sua periferia tem na sua extremidade um bloco de massa sobre uma superfície horizontal. O cabo é puxado por uma força constante , ergendo o bloco de uma altura , como mostra a figura. Desprezando-se o efeito de atrito entre o pino e o disco e considerando que o bloco e o disco estavam em repouso no momento em que a força começou a agira calcule:

1. A aceleração com que o bloco é erguido;
2. O módulo da tração que age sobre o trecho do cabo entre o disco e o bloco;
3. A energia cinética adquirida pelo disco imediatamente após o bloco ser erguido da altura .

Dado: o momento de inércia do disco para um eixo que passa perpendicularmente ao disco e pelo seu centro é .