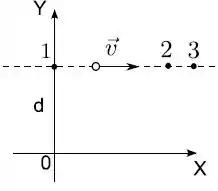
Uma partícula move-se com velocidade constante ao longo de uma reta paralela ao eixo que corta o em . Sejam , e os momentos angulares da partícula, relativos à origem , nos pontos , e , como indicados na figura. Os módulos dos momentos angulares são tais que

1. ;
2. ;
3. ;
4. ;
5. e ;

O momento angular é dado por:

Logo:

Para esse caso, temos:

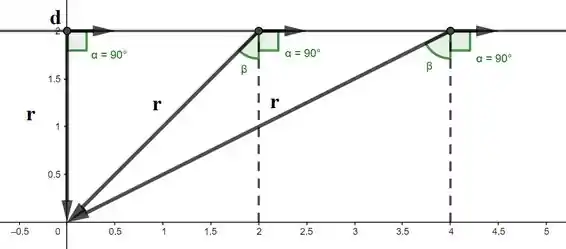
Note que:

Portanto:

E nota ainda o seguinte! O ângulo é sempre a ponta de um triângulo onde a hipotenusa é exatamente e a altura é sempre ! Logo:

A massa, a velocidade e a distância são as mesmas para todos os pontos, pois é a mesma partícula e ela ta sempre equidistante do eixo . O r, por sua vez, sendo o braço ou o módulo do vetor distância (que aponta pra origem), varia sempre. No entanto, o ângulo (entre o braço e a velocidade), mesmo mudando também constantemente, o fará a uma proporção que cancela a variação de ! Portanto temos que: .