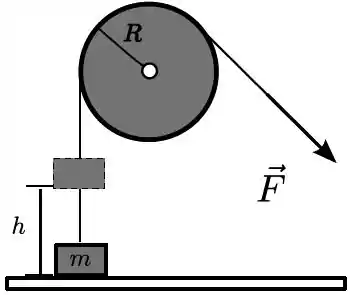
Um disco de raio e massa encontra-se fixado a uma parede vertical em um pino que passa pelo seu centro. Um cabo de massa desprezível passando pela sua periferia tem na sua extremidade um bloco de massa sobre uma superfície horizontal. O cabo é puxado por uma força constante , ergendo o bloco de uma altura , como mostra a figura. Desprezando-se o efeito de atrito entre o pino e o disco e considerando que o bloco e o disco estavam em repouso no momento em que a força começou a agira calcule:
- A aceleração com que o bloco é erguido;
- O módulo da tração que age sobre o trecho do cabo entre o disco e o bloco;
- A energia cinética adquirida pelo disco imediatamente após o bloco ser erguido da altura .
Dado: o momento de inércia do disco para um eixo que passa perpendicularmente ao disco e pelo seu centro é .
Passo 1
a)
Vamos começar fazendo o DCL do bloco
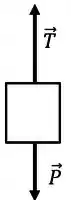
Considerando que o bloco está subindo, vamos chamar o módulo da aceleração do bloco de
Passo 2
Vamos agora ver as forças que produzem torque no disco, já que vamos nos preocupar só com a rotação
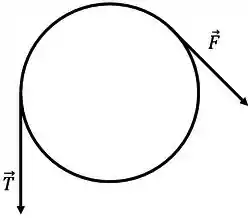
Vamos ter
Como já vimos o momento de inercia de um disco vai ser
Além disso como o bloco está subindo o disco roda no sentido horário, considerando o módulo a aceleração angular como . Além disso temos a relação
Isso tudo resulta em
Passo 3
Temos as equações
Somando as duas equações
Passo 4
A tração nesse ponto pode ser encontrada usando a primeira equação
Passo 5
c)
A energia cinética final é
Como o movimento do disco é com aceleração angular constante temos um movimento uniformemente variado, usando Torricelli
Usamos a equação de Torricelli porque a variação de energia cinética tem a diferença das velocidades angulares como a equação de Torricelli. Vamos ter
Passo 6
O momento de inércia já sabemos
Se o bloco sobe podemos relacionar essa altura com a variação angular do disco
Além disso temos a aceleração angular
Juntando tudo