Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento Angular

Ver Teoria
Exercício 951234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939496979899100

Enunciado

Momento Angular

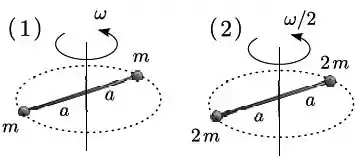
Dois alteres 1 e 2 mostrados na figura giram em torno de seus respectivos centros de massa em torno de um eixo fixo e perpendicular ao seu comprimento. O haltere 1 gira com velocidade angular constante ω e o haltere 2 com velocidade angular constante ω / 2 . No haltere 1 as massas de suas extremidades são iguais a m e no haltere 2 2 m . Os módulos de seus momentos angulares L 1 e L 2 em relação aos respectivos centros de massa e as suas energias cinéticas K 1 e K 2 cinéticas são relacionados respectivamente como

  1. L 1 = L 2 e K 1 > K 2
  2. L 1 = L 2 e K 1 = K 2
  3. L 1 = L 2 e K 1 < K 2
  4. L 1 < L 2 e K 1 < K 2
  5. L 1 > L 2 e K 1 > K 2

Passo 1

Considerando a massa dos halteres desprezíveis vamos calcular o momento angular e a energia cinética em cada halter Isso porque

L = I ω

K = I ω 2 2

Ou seja precisamos dos momentos de inércia já que já foi dado a velocidade angular

Passo 2

Começando pelo halter 1

I 1 = m a 2 + m a 2

I 1 = 2 m a 2

Vamos ter então

L 1 = I 1 ⋅ ω 1

L 1 = 2 m a 2 ⋅ ω

L 1 = 2 m ω a 2

E

K 1 = I 1 ⋅ ω 1 2 2

K 1 = 2 m a 2 ⋅ ω 2 2

K 1 = m a 2 ω 2

Passo 3

Agora para o halter 2

I 2 = 2 m a 2 + 2 m a 2

I 2 = 4 m a 2

Vamos ter então

L 2 = I 2 ⋅ ω 2

L 2 = 4 m a 2 ⋅ ω 2

L 2 = 2 m ω a 2

E

K 2 = I 2 ⋅ ω 2 2 2

K 2 = 4 m a 2 ⋅ ω / 2 2 2

K 2 = 4 m a 2 ω 2 / 4 2

K 2 = m a 2 ω 2 2

Passo 4

Então

L 1 = L 2

E

K 1 > K 2

Resposta

Letra A

Exercícios de Livros Relacionados

Um bloco homogênea de granito em forma de livro possui faces de 20c m por 15c m e uma espessura de 1,2c m . A massa específica (massa por unidade de volume) do granito é 2,64g / c m 3 . O bloco gira e
10.19E Calcule o momento angular orbital da Terra em termos da constante de Planck.
Um ponto na borda de um rebolo com 0,75m de diâmetro muda de velocidade, a uma taxa constante, de 12m / s para 25m / s em 6,2s . Qual é a aceleração angular média do rebolo?
Em um certo instante, uma partícula de 0,80k g está situada na posição r → = 2,0m i ^ + 3,0m j ^ . O momento linear da partícula está no plano x y e tem um módulo de 2,4k g ∙ m / s e uma direção de 11
Em um certo instante, a força F → = 4 j → N age sobre um objeto de 0,25 k g cujo vetor posição é r → = 2 i → - 2 k → e cujo vetor velocidade é v → = - 5 i → + 5 k → . Em relação à origem e em termos d