Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Cinética de Rotação

Ver Teoria
Exercício 231234567891011121314151617181920212224252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899

Enunciado

Rotação

Uma barra fina e homogênea de massa M e comprimento L é liberada na posição horizontal a partir do repouso e gira em torno de um eixo horizontal fixo, perpendicular a ela e que passa por uma de suas extremidades. Sabendo que não há atrito entre a barra e o eixo e que o momento de inércia da barra relativo ao eixo é igual a 1 / 3 M L 2 , podemos afirmar que ao passar pela posição vertical a velocidade do centro de massa da barra é

  1. 3 g L / 2 ;
  2. 3 g L ;
  3. π g L / 2 ;
  4. 3 g L / 4 ;
  5. π g L / 2 ;

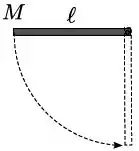
Passo 1

Já vimos que nesse caso a energia mecânica se conserva dessa forma

E m 0 = E m f

Lembrando que para corpos extensos, aqueles que o tamanho importa, a energia potencial gravitacional é calculada pelo centro de massa.

Passo 2

No início temos

E m 0 = U g 0

U g 0 = M g L

Porque o centro de massa está a uma altura l do chão

Passo 3

Na posição vertical

E m f = K f + U g f

Para a enérgica cinética vamos usar a fórmula com o momento de inércia em relação ao centro de rotação, porque isso já foi dado pelo enunciado

K f = I C R ⋅ ω 2 2

K f = 1 / 3 M L 2 ⋅ ω 2 2

K f = M L 2 ω 2 6

Passo 4

A energia potencial gravitacional final vai ver

U g f = M g ⋅ L 2 = M g L 2

Isso porque o centro de massa vai estar a uma altura L / 2 do chão

Então

E m f = K f + U g f

E m f = M L 2 ω 2 6 + M g L 2

Passo 4

Igualando as energias vamos ter

M g L = M L 2 ω 2 6 + M g L 2

Antes, o enunciado quer a velocidade do centro de massa. Lembrando que

v C M = R ⋅ ω

Nesse caso a distância entre o centro de massa e o centro de rotação é

R = L 2

Então

v C M = L ω 2

ω L = 2 v C M

Substituindo na equação da energia

M g L = M L 2 ω 2 6 + M g L 2

M g L = M 2 v C M 2 6 + M g L 2

M g L = 4 M v C M 2 6 + M g L 2

Passo 6

Resolvendo essa equação

M g L = 4 M v C M 2 6 + M g L 2

M g L 2 = 4 M v C M 2 6

3 g L 4 = v C M 2

v C M = 3 g L 4

Resposta

Letra D

Exercícios de Livros Relacionados

Uma régua de um metro é mantida verticalmente com uma das extremidades apoiada no solo e depois liberada. Determine a velocidade da outra extremidade pouco antes de tocar o solo, supondo que a extremi
Na figura abaixo, uma barra fina e homogênea (com 4 m de comprimento e uma massa de 3 k g ) gira livremente em torno de um eixo horizontal A que é perpendicular à barra e passa por um ponto situado a
O corpo rígido da figura abaixo é formado por três bolas e três barras de ligação, com M = 1,6 k g , L = 0,6 m e θ = 30 ° . As bolas podem ser tratadas como partículas e as barras têm massa desprezíve
Como estagiário de uma empresa de engenharia, você é solicitado a medir o momento de inércia de uma grande roda, para girar em torno de um eixo que passa pelo seu centro. Você mede o diâmetro da roda,
91 . Na F I G U R AP D 12.91 , uma bola de gude desce rolando um trilho que possui uma parte em loop com raio R . A bolinha possui massa m e raio r . Que altura mínima h deve ter o trilho a fim de que