Um projétil é lançado de uma plataforma do ponto e num dado instante após ser lançado ele se fragmenta em dois pedações de massa e , que caem simultaneamente nas posições horizontais e respectivamente. Se o projétil não se fragmentasse o seu alcance seria,
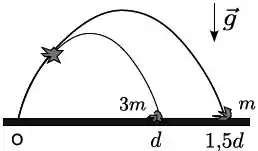
- ;
- ;
- ;
- ;
- ;
Passo 1
Quando temos uma explosão, já vimos que o centro de massa mantém o movimento que ele estava tendo antes da explosão. A posição que ele cairia sem se fragmentar seria a posição do centro de massa. Vamos nos preocupar apenas com o , porque sabemos que na queda o centro de massa estará no chão.
Passo 2
A fórmula do centro de massa é
Pelos dados no enunciado
E
Então
Resposta
Letra E