P2 de Física 1 da UFRJ - 2015.2

Um tenista realiza um saque arremessando a bola verticalmente até uma altura máxima h em relação ao solo, na qual atinge a bola com a raquete. A bola sai com velocidade horizontal e suficiente para voar até atingir o solo a uma distância horizontal A da posição de saque. Sabendo que o tempo de colisão entre a raquete e a bola é ∆t e que a massa da bola é m, a força média exercida pela raquete sobre a bola durante o intervalo ∆t é:

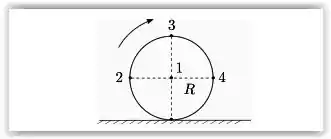
Uma esfera rígida homogênea de raio R rola sem deslizar sobre uma superfície horizontal com velocidade angular ω constante e velocidade do centro de massa . A figura mostra quatro pontos na superfície da esfera contidos no plano vertical da velocidade . Considere , , e os vetores velocidade dos pontos 1, 2, 3 e 4, respectivamente. A resposta correta é:

Dois cilindros rígidos homogêneos, A e B, rolam sem deslizar sobre uma superfície horizontal, com a mesma velocidade angular constante de módulo ω. As relações entre as massas e os raios dos cilindros são e e. O momento de inércia de um cilindro homogêneo de massa M e raio R relativo ao seu eixo, que passa pelo centro de massa, é . Sendo e a energia cinética total e o módulo da velocidade do centro de massa do cilindro A, e e as do cilindro B, podemos dizer que:

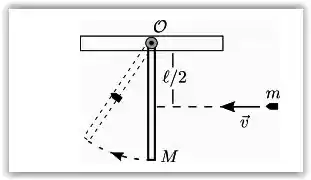
A figura mostra uma barra homogênea de massa M e comprimento que se encontra em repouso na posição vertical, presa ao teto pela sua extremidade superior, podendo girar livremente em um plano vertical em torno de um eixo horizontal OZ (perpendicular ao plano da figura). Um projetil de massa m, e dimensões desprezíveis, move-se no mesmo plano vertical e atinge a barra com velocidade horizontal de modulo v, alojando-se em seu ponto médio. Calcule:

1. o momento de inercia da barra relativo ao eixo OZ sabendo que o seu momento de inercia relativo a um eixo ortogonal a ela e que passa pelo seu centro é dado por
2. o módulo do momento angular do projétil em relação ao ponto O imediatamente antes da colisão;
3. o momento de inercia do sistema barra + projetil relativo ao eixo OZ após a colisão;

d) a velocidade angular adquirida pelo sistema barra + projétil imediatamente após a colisão;

e) a energia mecânica perdida pelo sistema no processo de colisão

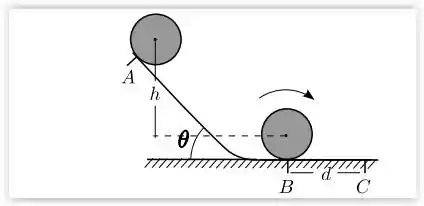
A figura mostra uma rampa constituída por um trecho plano, inclinado de um angulo em relação à horizontal, que se conecta suavemente a um trecho plano horizontal. Um cilindro homogêneo de massa e raio é liberado a partir do repouso em um ponto A do plano inclinado e desce percorrendo a rampa passando pelos pontos B e C do trecho horizontal, rolando sem deslizar durante todo o trajeto; de A para B o centro de massa desce uma altura . Lembrando que o momento de inércia do cilindro relativo ao seu eixo de simetria perpendicular às bases , calcule:

a) a aceleração do centro de massa do cilindro, enquanto ele desce o plano inclinado;

b) a força de atrito (modulo, direção e sentido) que age no cilindro enquanto ele desce o plano inclinado;

c) a velocidade do centro de massa do cilindro ao passar pelo ponto B;

d) o trabalho realizado por cada uma das forças que agem sobre o cilindro, quando seu centro de massa se desloca de uma distância entre os pontos B e C.

Um objeto A de massa e velocidade de módulo colide com outro objeto B de massa , inicialmente em repouso. As velocidades dos objetos antes e depois da colisão têm a mesma direção e a colisão ocorre em um intervalo de tempo ∆t. Se o módulo da força média nesse intervalo exercida pelo objeto A sobre o B é f, o valor de ∆t para que a colisão seja perfeitamente inelástica é:

Um carrossel de raio R e momento de inércia I em relação ao eixo de rotação está girando, sem atrito, com velocidade angular ω constante ao redor do eixo vertical, que passa perpendicularmente pelo seu centro. Uma criança de massa m, que está inicialmente em repouso no solo, salta sobre o carrossel e consegue sentar na sua borda e aí permanece. A nova velocidade angular do carrossel é:

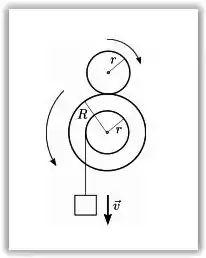
Duas polias dentadas estão conectadas sem que ocorra deslizamento entre elas. A polia menor possui raio r e a maior, raio R. A polia maior está conectada a um objeto através de um fio ideal e uma engrenagem interna de raio r, conforme a figura. Em um dado instante, o objeto desce verticalmente com velocidade v. Nesse instante, a velocidade angular da polia menor é dada por:

Um pêndulo é constituído por uma partícula de massa m e um fio ideal de comprimento d preso ao teto em um ponto de fixação O. A partícula é solta a partir do repouso com o fio tensionado e fazendo um ângulo θ com a vertical (posição A). Quando o fio passa pela posição vertical a partícula tem uma velocidade de módulo v. Tomando todos os momentos angulares e torques relativos ao ponto de fixação O, denotando por e os momentos angulares da partícula nas posições A e B, e por e os torques sobre a partícula nas posições A e B, respectivamente, podemos afirmar que:

1. e
2. e
3. e
4. e
5. e