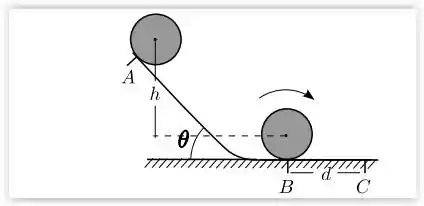
A figura mostra uma rampa constituída por um trecho plano, inclinado de um angulo em relação à horizontal, que se conecta suavemente a um trecho plano horizontal. Um cilindro homogêneo de massa e raio é liberado a partir do repouso em um ponto A do plano inclinado e desce percorrendo a rampa passando pelos pontos B e C do trecho horizontal, rolando sem deslizar durante todo o trajeto; de A para B o centro de massa desce uma altura . Lembrando que o momento de inércia do cilindro relativo ao seu eixo de simetria perpendicular às bases , calcule:
a) a aceleração do centro de massa do cilindro, enquanto ele desce o plano inclinado;
b) a força de atrito (modulo, direção e sentido) que age no cilindro enquanto ele desce o plano inclinado;
c) a velocidade do centro de massa do cilindro ao passar pelo ponto B;
d) o trabalho realizado por cada uma das forças que agem sobre o cilindro, quando seu centro de massa se desloca de uma distância entre os pontos B e C.
Passo 1
Primeiramente, vamos entender as forças que agem sobre o cilindro quando ele está no plano inclinado.
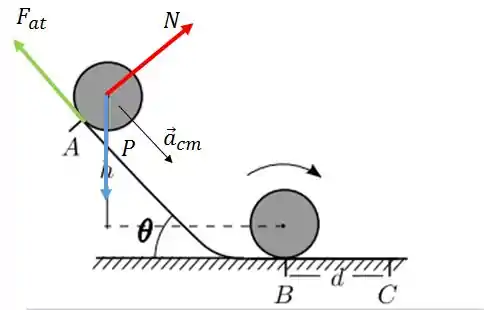
é a força de atrito
é a normal
é a força peso
é a aceleração do centro de massa do cilindro
Passo 2
Show! Com o diagrama de forças feito e, sabendo que o cilindro desce sem deslizar sobre o plano inclinado, podemos formular duas equações, uma de translação e outra de rotação.
A de translação é a clássica segunda lei de Newton:
Translação:
A de rotação é aquela que relaciona torque com momento de inércia e aceleração angular:
Rotação:
Além disso, a gente já sabe que quando o cilindro rola sem deslizar temos aquela relação entre aceleração do centro de massa e aceleração angular:
Agora, precisamos manipular essas equações. Para isso, vamos decompor a força peso em e e definir os eixos x,y e z, conforme a figura abaixo:
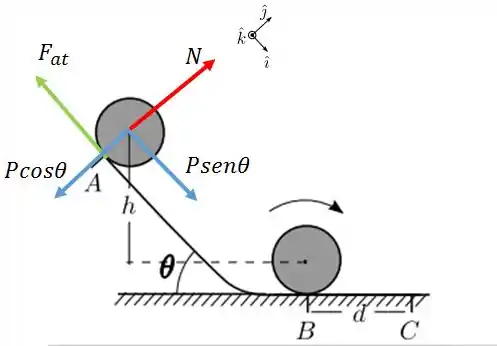
Para translação:
Para rotação:
Aqui percebemos que os torques em relação ao centro do cilindro gerados pela força normal e pela força peso são nulos. Basta perceber que a linha de atuação de ambas as forças passa pelo eixo de rotação. Logo, só teremos torque gerado pela força de atrito.
Considerando o sentido anti-horário positivo, montamos a seguinte equação:
Continuando a manipulação das equações, aplicando na equação de rotação, montamos o sistema:
Resolvendo esse sistema, chegamos em:
O problema nos fornece o momento de inércia do cilindro que vale:
Substituindo por , chegamos a
Passo 3
Agora, vamos achar a força de atrito. Lembra que tínhamos chegado nessa equação?
Então, agora é só substituir o valor que achamos para e o valor de para o cilindro. Chegamos, então, em:
Falta entender qual é a direção e sentido da . Como o sinal deu positivo, podemos perceber que arbitramos inicialmente o sentido certo de . Caso tivesse dado um resultado negativo, teríamos a força de atrito estaria no sentido contrário ao que arbitramos.
Passo 4
Show! Agora precisamos achar a velocidade do cilindro ao passar pelo ponto B.
Vamos aplicar a famosa conservação da energia mecânica para o trecho A-B. Podemos supor que não temos energia potencial gravitacional no final, quando o cilindro chega do plano inclinado, partindo do pressuposto que a linha de referência passa pelo centro de massa do cilindro, conforme mostrado na figura.
Assim, no início (ponto A) só temos Energia Potencial, já que o cilindro ainda não está em movimento e, no final, só temos Energia de Cinética de rotação e Energia Cinética de translação.
Como o cilindro rola sem deslizar, podemos fazer a relação , ou seja, .
Podemos também utilizar o momento de inércia dado no enunciado novamente: .
Manipulando , chegamos a:
Igualando a , chegamos a:
Passo 5
As forças que agem sobre o cilindro no trecho B – C são o peso , a e a
A sacada aqui está em perceber que ambos são nulos, pois ambas as forças são perpendiculares ao deslocamento do cilindro.
Nesse trecho não teremos por que as velocidades angular e de translação do cilindro são constantes. Se houvesse nesse trecho haveria desaceleração e torque sobre o cilindro, assim o trabalho da nesse trecho é nulo também