Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Rolamento sem Deslizamento

Ver Teoria
Exercício 321234567891011121314151617181920212223242526272829303133343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFRJ, Física 1, Prova 2, 2015.2

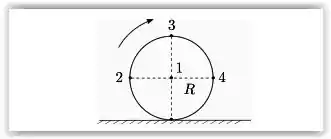
Uma esfera rígida homogênea de raio R rola sem deslizar sobre uma superfície horizontal com velocidade angular ω constante e velocidade do centro de massa V → C M . A figura mostra quatro pontos na superfície da esfera contidos no plano vertical da velocidade V → C M . Considere v 1 → , v 2 → , v 3 → e v 4 → os vetores velocidade dos pontos 1, 2, 3 e 4, respectivamente. A resposta correta é:

  1. v 2 → = v 4 → = w R 2
  2. v 1 → = v 2 → = v 4 → = | V → C M |
  3. v 2 → = v 4 →
  4. v 1 → + v 3 → = 2 V → C M
  5. v 2 → = v 4 → = w R

Passo 1

Numa rotação a velocidade de um ponto é:

v = R . w

Onde R é a distância do centro de rotação até aquele ponto.

Já vimos que quando alguma coisa rola sem deslizar pelo chão o ponto de contato com o chão tem velocidade igual a zero, porque ele é o ponto de rotação.

Vamos, então analisar a velocidade em cada ponto:

R 1 = R 2 = R 2 + R 2 = R   √ 2

R 3 = 2 R

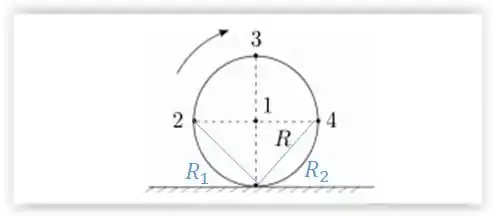
Passo 2

Agora, só substituir na equação abaixo de acordo com o R em cada ponto:

v = R . w

v 1 = R . w = | V → C M |

v 2 = R √ 2 w

v 3 = 2 R w

v 4 = R √ 2 w

Assim, a resposta é a letra A:

v 2 → = v 4 → = w R 2

Resposta

a) v 2 → = v 4 → = w R 2

Exercícios de Livros Relacionados

Um mecanismo em forma de ioiô, montado em um eixo horizontal sem atrito, é usado para levantar uma caixa de 30kg , como mostra a figura abaixo. O raio externo R da roda é 0,5m e o raio r do cubo da ro
Na Fig. 11-60, uma força horizontal constante F → de módulo 12N é aplicada a um cilindro maciço homogêneo através de uma linha de pescar enrolada no cilindro. A massa do cilindro é 10k g , o raio é 0,
10.3E Um cilindro rola em uma rampa de inclinação θ = 30 ° . A) Calcule a aceleração angular do cilindro B) Calcule a força de atrito da rampa sobre o cilindro.
10.7P Calcule em termos do raio R da bola, o parâmetro de impacto b de uma tacada com que um jogador deve chutar uma bola para que esta tenha uma velocidade angular vertical dada por ω = v / 2 R .
Um ioiô possui um momento de inércia de 950 g c m ² ² e uma massa de 120 g . O raio do eixo é 3,2 m m e a corda tem 120 c m de comprimento. O ioiô rola para baixo, a partir do repouso, até a extremida