UFRJ, Física 1, Prova 2, 2015.2
Um pêndulo é constituído por uma partícula de massa m e um fio ideal de comprimento d preso ao teto em um ponto de fixação O. A partícula é solta a partir do repouso com o fio tensionado e fazendo um ângulo θ com a vertical (posição A). Quando o fio passa pela posição vertical a partícula tem uma velocidade de módulo v. Tomando todos os momentos angulares e torques relativos ao ponto de fixação O, denotando por e os momentos angulares da partícula nas posições A e B, e por e os torques sobre a partícula nas posições A e B, respectivamente, podemos afirmar que:
- e
- e
- e
- e
- e
Passo 1
Na posição A, a partícula está em repouso e como sabemos que a fórmula do momento angular é:
Esse momento será nulo, pois a velocidade é nula.
Passo 2
Primeiramente, vamos analisar o torque na posição A:
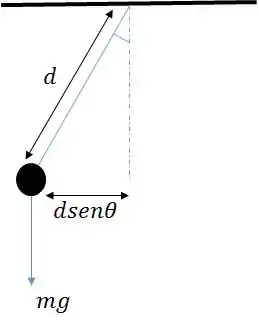
Como a tração não gera torque, pois a linha de ação da sua força passa pelo eixo de rotação, a única força que gera torque é a força peso . A distância da linha de ação da força mg até a o eixo de rotação é dada por , conforme mostra a figura.
Assim, podemos calcular o módulo do torque gerado por na posição A:
Resposta
e