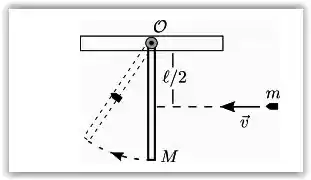
A figura mostra uma barra homogênea de massa M e comprimento que se encontra em repouso na posição vertical, presa ao teto pela sua extremidade superior, podendo girar livremente em um plano vertical em torno de um eixo horizontal OZ (perpendicular ao plano da figura). Um projetil de massa m, e dimensões desprezíveis, move-se no mesmo plano vertical e atinge a barra com velocidade horizontal de modulo v, alojando-se em seu ponto médio. Calcule:
- o momento de inercia da barra relativo ao eixo OZ sabendo que o seu momento de inercia relativo a um eixo ortogonal a ela e que passa pelo seu centro é dado por
- o módulo do momento angular do projétil em relação ao ponto O imediatamente antes da colisão;
- o momento de inercia do sistema barra + projetil relativo ao eixo OZ após a colisão;
d) a velocidade angular adquirida pelo sistema barra + projétil imediatamente após a colisão;
e) a energia mecânica perdida pelo sistema no processo de colisão
Passo 1
Primeiramente, é pedido o momento de inércia da barra relativo ao eixo Oz. Como o momento de inércia do centro de massa é dado no enunciado, podemos aplicar o teorema dos eixos paralelos:
No caso do problema, temos:
Assim, chegamos a:
Passo 2
O momento angular é dado pelo produto vetorial:
Logo, seu módulo é dado por:
Sendo o ângulo formado pela direção da velocidade e pelo vetor posição em relação ao eixo que se refere.
Como vemos pela figura que o ângulo formado pela direção da velocidade do projétil e pelo vetor posição do projétil no momento da colisão em relação ao ponto O é de , o vale 1.
Além disso, sabemos que (vetor posição do ponto de colisão em relação ao ponto ) vale .
Então, L será:
Show? Vamo que vamo!
Passo 3
Agora vamos calcular o momento de inércia do sistema barra + projétil relativo ao eixo O após a colisão.
A sacada aqui está no fato do projétil ter dimensões desprezíveis e, dessa forma, podemos trata-lo como uma partícula.
Dessa forma, seu momento de inércia após a colisão será dado por:
Como achamos no passo 1, podemos achar o momento de inércia total do sistema barra + projétil em relação a O.
Passo 4
Para analisar essa questão vamos começar enunciando aquela relação entre momento angular e torque externo:
Com outras palavras, essa forma significa que o torque externo resultante é igual a variação do momento angular em relação ao tempo.
Vamos analisar o torque resultante?
Imediatamente após a colisão quais são as forças que atuam na barra?
A força peso e a força de sustentação em sentidos opostos. Mas, ambas têm sua linha de ação de força passando pelo eixo O, logo, não geram torque, repare:
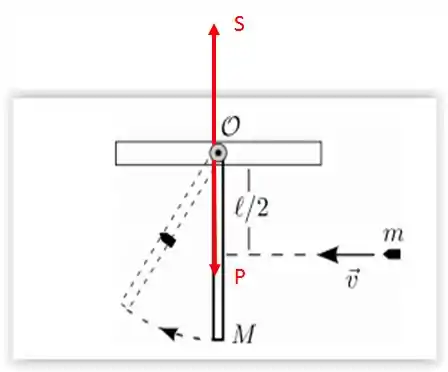
Como o torque imediatamente após a colisão é nulo, podemos dizer que o momento angular do sistema se conserva.
O nós já temos. Como a barra está parada, seu momento angular inicial é nulo. Temos apenas o momento angular do projétil antes da colisão e já o calculamos:
O problema pede a velocidade angular adquirida logo após a colisão, certo? Então, podemos aplicar a outra fórmula para momento angular, utilizada para corpos extensos:
Como vamos utilizar essa fórmula para o , o utilizado será o do sistema barra + projétil. Assim montamos a equação:
Igualando os dois:
Passo 5
É possível perceber que se trata de uma colisão inelástica, já que parte da energia do sistema foi perdida durante a colisão.
No entanto, sabemos que inicialmente só há a energia cinética de translação do projétil. No final, só há a energia cinética de rotação do sistema.
Dessa forma,
Aqui, substituímos os valores que achamos até aqui:
Chegamos, então, a: