Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Polias Não-Ideais

Ver Teoria
Exercício 2212345678910111213141516171819202123242526272829303132333435363738394041424344454647

Enunciado

UFRJ, Física 1, Prova 2, 2015.2

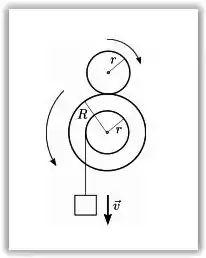
Duas polias dentadas estão conectadas sem que ocorra deslizamento entre elas. A polia menor possui raio r e a maior, raio R. A polia maior está conectada a um objeto através de um fio ideal e uma engrenagem interna de raio r, conforme a figura. Em um dado instante, o objeto desce verticalmente com velocidade v. Nesse instante, a velocidade angular da polia menor é dada por:

  1. R r 2   v
  2. r R 2   v
  3. 1 r   v
  4. 1 R   v
  5. R - r r 2   v

Passo 1

Vamos entender o problema primeiro.

A gente tem a velocidade linear da engrenagem interna de raio r e sabemos que:

Numa rotação a velocidade de um ponto é:

v = R . w

Onde R é a distância do centro de rotação até aquele ponto.

Assim, descobrimos que a velocidade angular da engrenagem interna vale

w e n g = v r

Passo 2

Vamos entender agora o que está acontecendo. A polia maior e a engrenagem interna fazem o mesmo número de voltas num determinado tempo, já que elas giram juntas.

Assim, elas têm a mesma frequência e, por consequência, a mesma velocidade angular.

w p o l i a m a i o r = w e n g

w p o l i a m a i o r = v r

Passo 3

Show!

Vamos descobrir agora a velocidade linear da polia maior aplicando

v = R . w

v p o l i a m a i o r = R . w p o l i a m a i o r

v p o l i a m a i o r = R r v

Passo 4

Agora vamos relacionar com a polia menor. A gente sabe que no ponto de contato a velocidade linear da polia maior é igual à velocidade linear da polia menor.

Então, podemos montar:

v p o l i a m e n o r = v p o l i a m a i o r

A velocidade angular da polia menor será dada novamente pela fórmula:

v = R . w

v p o l i a m e n o r = r w p o l i a m e n o r

R r v = r w p o l i a m e n o r

w p o l i a m e n o r = R r 2 v

Resposta

  1. R r 2   v

Exercícios de Livros Relacionados

Um dispositivo para medir o momento de inércia de um corpo é mostrado na figura. A plataforma circular está presa a um tambor concêntrico de raio R , plataforma e tambor estando livres para girar em t
Um cilindro de uniforme, de massa M e raio R , tem um fio enrolado no seu entorno. O fio é mantido fixo, enquanto o cilindro cai verticalmente, como mostrado na figura. (a) Mostre que a aceleração do
A extremidade superior do fio enrolado em redor do cilindro da figura está segura por uma mão que acelera para cima, de modo que o centro de massa do cilindro não se move, enquanto o cilindro gira. De
Calcule o efeito da massa M da polia, de raio R , sobre o sistema do Cap. 4, Probl. 12 (fig); a masssa m , que desliza sem atrito está ligado à massa suspensa m ' pelo fio que passa sobre a polia. Det
Um bloco de massa m , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação θ em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio R e massa M ,