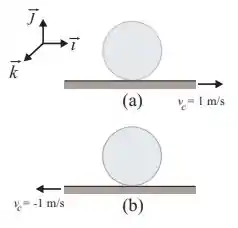
Um cilindro de raio rola sem deslizar com velocidade angular sobre uma correia móvel sob as condições mostradas na figura. No caso (a), a correia move-se com velocidade . No caso (b), a correia move-se com velocidade . Pode-se afirmar que as velocidades do centro do cilindro nos casos (a) e (b) são, respectivamente:
Passo 1
Cara... Imagina um disco girando sem deslizar, porém em cima de uma correia parada ()...

De acordo com a teoria, então se o disco gira sem deslizar com velocidade angular então o disco (ou o seu centro de massa) terá uma velocidade para a direita que depende apenas do raio e do módulo da velocidade angular ...
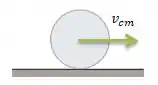
Agora, porque ele está se movimentando pra a direita e não para a esquerda?
Simples... Regra da mão direita! Sabemos que (o dedão) está apontado na direção de (para dentro da tela), então pela regra da mão direita, os demais dedos apontam no sentido horário de rotação, logo o disco só pode estar girando para a direita mesmo, saca?
Mas ainda você pode se perguntar...
“Tá beleza, mas isso é considerando que a correia tem velocidade , certo? Mas e se a correia tiver uma velocidade não nula ? Qual será a velocidade do centro de massa?”
Passo 2
Bem, nesse caso, é só imaginar: o que acontece se além da velocidade , a correia estivesse numa velocidade para a direita...
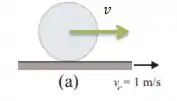
Nesse caso, a velocidade final do centro de massa seria simplesmente a soma das duas velocidades, isto é...
Como ...
O problema nos disse que ou , e ainda sabemos que é o módulo da velocidade angular , ou seja, ...
Passo 3
Agora, e se o chão (a correia) estivesse indo para trás com velocidade de...
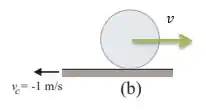
Ora, nesse caso novamente é somar as duas velocidades...
A diferença é que agora é negativa...
Resposta
Letra C