Um canhão é montado firmemente sobre um carrinho com rodas sem atrito, que está inicialmente em repouso em uma superfície horizontal lisa. O canhão dispara uma bala para a direita com uma velocidade , que é então capturada por um anteparo firmemente preso ao carrinho. Podemos afirmar que a velocidade final do sistema (constituído pelo carrinho+anteparo+canhão+bala) é:
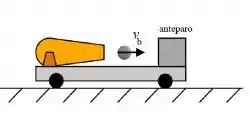
- , para a esquerda.
- , para a direita.
- .
- , para a esquerda.
- , para a direita.
Passo 1
Cara... Anota uma coisa aí no seu caderno de estudos: toda vez que um problema vier de velocidade inicial de um objeto e depois te pedir a velocidade final de alguma outra coisa (tipo a velocidade final do sistema como é pedido aqui) é porque provavelmente é uma questão que se resolve por conservação da quantidade de movimento linear.
Essa teoria maravilhosa aí nos afirma que se não tiver ação de uma força externa, o momento se conserva, isto é...
E vamos usar isso para encontrar a velocidade pedida, ta legal?
Passo 2
Cara, queremos saber qual é a velocidade do sistema, e pela teoria...
Onde é a massa do que você estiver analisando. Então se estamos analisando o sistema, . Então...
E para o momento final...
Onde é a velocidade inicial do sistema e é a velocidade final do sistema (que o problema está chamando de simplesmente )...
Agora vamos analisar essa equação com mais detalhes, pode ser?
Passo 3
Cara! Molha que interessante, o problema nos disse que o sistema...
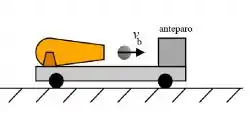
Antes de a bolinha sair (ou seja, inicialmente) estava parado! O que ele quer dizer com isso? Ele quer dizer que a velocidade inicial do sistema é ...
Então, por conservação do momento linear...
Como a massa do sistema não pode ser ...
Ou seja, a velocidade final do sistema é independente da velocidade do canhão, saca?! Ele colocou a bala ali só para confundir mesmo, porque o que importa para o problema é o sistema e não a bala rsrs.
Resposta
Letra C.