Uma partícula de massa move-se apenas sob a ação de uma força conservativa , onde é medido em metros e em Newtons. A variação da energia cinética da partícula quando ela se move da posição para a posição é:
(a)
(b)
(c)
(d)
(e)
Passo 1
FALA AÍ! Tudo bom?
Bem... O problema não nos deu um desenho maroto, então é por aqui que devemos começar... Shall we?
Temos uma partícula se movendo no plano sob ação de uma força que atua na direção de ( a componente indica que é exclusivamente na direção de )...
De acordo com a nossa Teoria, a variação do trabalho é igual a variação da energia cinética que estamos buscando no problema, isto é...
Onde o trabalho de uma força pode ser sempre calculado pela integral de linha...
Onde é o caminho percorrido pela partícula. é o vetor tangente a essa direção.
Mas pera aí... Qual é o caminho percorrido pela partícula?
Passo 2
ORA! O problema nos disse apenas que a partícula se desloca de até , mas ele não fala nada sobre o caminho que ela faz até chegar .
Entretanto, todavia, contudo, não obstante... O problema também nos fala que a força é conservativa! Isto é, independe do caminho que ela andar!
Aí agora pensa comigo, se independendo do caminho que escolhermos, vamos encontrar o mesmo valor para o trabalho , podemos escolher para a solução do problema, a curva mais simples possível... Uma reta ligando até ...
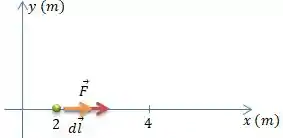
Passo 3
Essa reta é tão interessante, porque ela simplifica muito os cálculos! Veja bem, sabemos que é o vetor tangente na direção que estamos andando. Quem é esse vetor tangente na reta?
ISSO MESMO! O vetor é um vetor exclusivamente na direção de (direção ), então o módulo dele inclusive será o mesmo que o módulo de (), então...
E isso é interessante, porque na integral de linha fazemos a integração do produto escalar...
E o produto escalar de dois vetores quaisquer... , então...
Só que varia de até na reta, então, podemos calcular a integral de linha agora...
Passo 4
Resolvendo a integral...
Substituindo os limites de integração...
Simplificando...
Então, a variação de energia cinética é...
Resposta
Letra A