Em um dado instante , observa-se que duas partículas de massas e estão nas posições e movendo-se com velocidades e , respectivamente. Passados , elas são novamente observadas e vê-se que encontra-se parada. Sabendo-se que elas estão sujeitas somente a forças internas, o vetor posição do centro de massa (em metros) quando é:
(a)
(b)
(c)
(d)
(e)
Passo 1
Cara, que tal desenharmos esse sistema aí para termos uma noção do que está acontecendo?
Bem, o problema nos disse que no tempo , temos duas partículas e que estão localizadas nas posições e ...
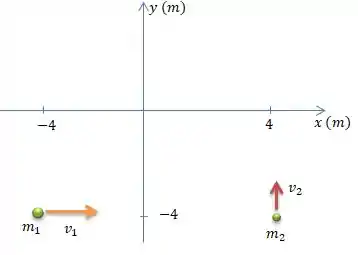
Nesse momento, o sistema possui um centro de massa cuja posição ta um pouco mais próxima da massa por ela ser mais pesada...
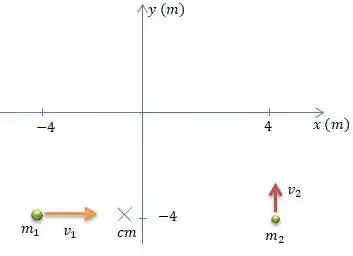
Esse centro de massa possui uma velocidade e ele vai ser muito útil para resolvermos o problema. Mas o que o problema quer afinal?
Bem, ele quer que passados a gente encontre a nova posição do centro de massa .
Ora, como não existem forças externas (apenas interna) o centro de massa vai permanecer numa velocidade constante o tempo todo, isso significa que pela cinemática, podemos encontrar a nova posição do centro de massa por , mas nesse caso, queremos ...
Então repare que para encontrar a posição do centro de massa no tempo , precisamos primeiro determinar qual é a velocidade e também quem é . Vamos nessa?
Passo 2
VELOCIDADE DO CENTRO DE MASSA...
Cara, como já comentamos, a velocidade do centro de massa permanecerá constante, já que não há forças externas empurrando as massas. Isso é o mesmo que dizer que o momento de inércia das massas se mantêm constantes, saca?
De acordo com a teoria, quando isso acontece, podemos calcular a velocidade do centro de massa pela fórmula...
Então, substituindo os dados do enunciado...
Passo 3
Agora, vamos encontrar (a posição inicial do centro de massa). É essa posição marcada com aqui...
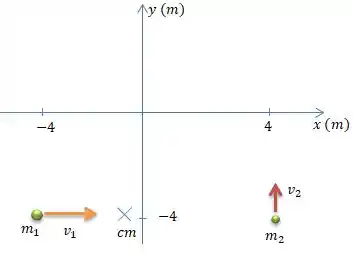
Para encontrar isso, basta lembrar que centro de massa pode ser obtido por...
Então...
Simplificando...
Passo 4
Bem, para encontrar a posição do centro de massa então passados ...
Então...
Resposta
Letra E.