Dois objetos estão se movendo como mostra a figura ao lado. O objeto de massa move-se com vetor velocidade que faz um ângulo de com o eixo . O objeto de massa move-se com vetor velocidade que faz um ângulo de com o eixo . O valor do momento angular total em torno do ponto O é (no SI):
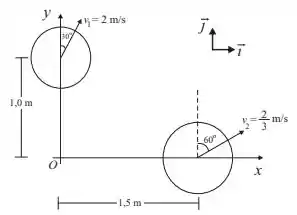
Passo 1
Cara... De acordo com a nossa teoria, o momento angular total é a soma dos momentos angulares de cada objeto. Assim, o momento angular total do sistema será...
Onde representa o momento angular do primeiro objeto e o do segundo...
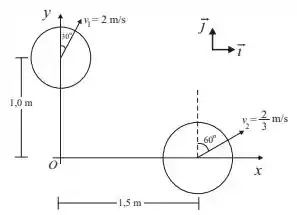
Ainda de acordo com a nossa amada teoria, o momento angular em relação a origem de cada objeto pode ser calculado por...
Onde e são os vetores posição de cada objeto...
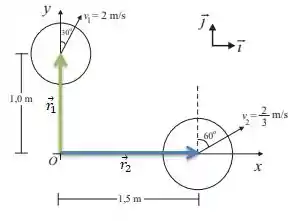
Agora, conhecendo os vetores e de cada objeto podemos passar para o cálculo! Bora?
Passo 2
MOMENTO ANGULAR ...
De acordo com a teoria ainda, podemos calcular o módulo do momento angular pela expressão...
Onde é o ângulo entre e , ou seja, no caso da primeira massa esse ângulo é . Substituindo os valores dados no problema, sabendo que ...
Só que agora você tem que ficar atento ao sinal desse momento angular. Pela regra da mão direita entre o vetor e (girando os dedos do eixo onde está o até o ) observamos que o dedão apontará para dentro da tela, isso significa que é um vetor para dentro da tela (na direção ou )...
Passo 3
Fazendo o mesmo para o objeto ...
No caso da segunda massa esse ângulo é . Substituindo os valores dados no problema, sabendo que ...
E esse vetor é realmente positivo, afinal pela regra da mão direita, vamos ver que esse vetor aponta para cima no eixo (direção )...
Somando os dois...
Resposta
Ei, a resposta está no passo a passo :)