Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo do Momento de Inércia em Corpos Extensos

Ver Teoria
Exercício 33123456789101112131415161718192021222324252627282930313234

Enunciado

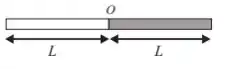
Uma barra homogênea de comprimento L   é emendada a outra de mesmo comprimento, também homogênea, mas com o dobro da massa, conforme a figura.

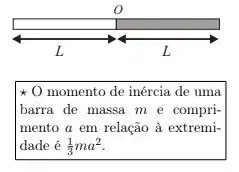
O símbolo O na figura marca o ponto da emenda. Quando m e 2 m representam as massas das barras, o momento de inércia e a distância do centro de massa do sistema em relação ao ponto de emenda valem, respectivamente:

  1. 1 3 m L 2         e     1 3 L
  2. 1 3 m L 2         e     1 6 L
  3. m L 2             e     1 3 L
  4. m L 2             e     1 6 L
  5. 2 m L 2         e     1 6 L

Passo 1

Bem... Sabemos pela dica do enunciado que o momento de inércia de uma barra de massa m e comprimento a em relação à extremidade...

É então dada por...

I = 1 3 m a 2

ORA! Não sei se você concorda, mas podemos considerar o problema de encontrar o momento de inércia da figura em relação ao ponto O ( I o )...

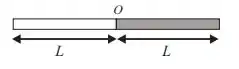
Como sendo a soma de dois momentos de inércia com relação à extremidade: momento de inércia da barra 1 e momento de inércia da barra 2 (a barra cinza). Ou seja...

I o = I 1 + I 2

Vamos nessa?

Passo 2

MOMENTO DE INÉRCIA DA BARRA 1:

POW! A Barra 1 é a barra branquinha de massa m ...

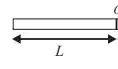
O momento de inércia dele em relação ao ponto O (extremidade dela) pode então ser dado como...

I 1 = 1 3 m a 2

Só que no nosso caso, a = L (comprimento da barra)...

I 1 = 1 3 m L 2

MOMENTO DE INÉRCIA DA BARRA 2:

Para a barra 2 vai ser basicamente a mesma coisa, mas dessa vez, a Barra 2 (barra cinza)...

Tem massa 2 m , então...

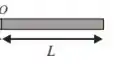
I 2 = 1 3 2 m L 2   →

I 2 = 2 3 m L 2

CONCLUSÃO:

Bem, como já falamos no passo 1 o momento de inércia final (momento de inércia do conjunto em relação ao ponto O )...

Vai ser a soma dos dois momentos de inércia encontrados...

I o = I 1 + I 2   →

I o = 1 3 m L 2 + 2 3 m L 2   →

I o = 3 3 m L 2   →

Logo...

I o = m L 2

Passo 3

CALMA JOVEM! Nosso problema ainda não acabou! Também temos que encontrar a distância do centro de massa ( x c m ) em relação ao ponto O ...

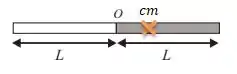
Repare que como a barra cinza é mais pesada que a barra branca, o centro de massa vai estar mais para a esquerda, e o que queremos é justamente a distância que ele está do ponto O ...

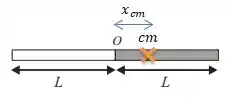
E como que nós podemos encontrar esse cara?

Passo 4

De acordo com a teoria de centro de massa, podemos determinar o centro de massa de um conjunto de objetos fazendo...

x c m = m 1 x 1 + m 2 x 2 m 1 + m 2

Onde m 1 e m 2 representam as massas desses objetos (no nosso caso são as massas das barras branca e cinza). x 1 e x 2 por sua vez são os centros de massas de cada uma dessas barras individualmente...

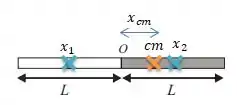
E olha que maneiro, sabemos que o centro de massa de uma barra homogênea, como a barra branca ou a cinza, fica exatamente na metade da barra. Então, se a gente considerar o ponto O como a origem das coordenadas...

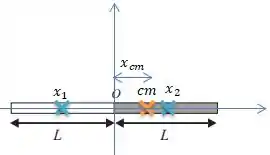
Então...

x 1 = - L 2         e         x 2 = L 2

Logo, sabendo que m 1 = m e m 2 = 2 m ...

x c m = m 1 x 1 + m 2 x 2 m 1 + m 2   →

x c m = m - L 2 + 2 m L 2 3 m   →

x c m = m L 2 3 m   →

Ou seja...

x c m = L 6  

Resposta

Letra D

Exercícios de Livros Relacionados

(a) Mostre que o momento de inércia de um cilindro maciço de massa M e raio R em relação ao eixo central é igual ao momento de inércia de um aro fino de massa M e raio R / 2 em relação ao eixo central
Use integração para determinar o momento de inércia de um disco fino uniforme de massa M e raio R em relação a um eixo do plano do disco que passa pelo seu centro. Confira sua resposta referindo à tab
Use integração para determinar o momento de inércia, em relação ao seu eixo, de um cone circular reto uniforme de altura H , raio da base R e massa M .
Um cilindro de massa M e raio R possui uma densidade que cresce linearmente a partir do seu eixo, ρ = α r , onde α é uma constante positiva. a) Calcule o momento de inércia do cilindro em relação a um
9.19E Calcule o momento de inércia de um cubo homogêneo de massa M e aresta a em relação a um eixo passando por uma de suas arestas.