P1 de Física 2 da UFRJ - 2016.1

A respeito da entropia de um gás, analise a alternativa INCORRETA:

1. Se o gás é resfriado a volume constante, sua entropia diminui.
2. Se o gás se expande a temperatura fixa, sua entropia aumenta.
3. Se o gás realiza um ciclo irreversível, sua entropia aumenta.
4. A entropia do gás não se altera em uma expansão adiabática reversível.

Para um dado processo termodinâmico, a capacidade térmica de um corpo varia com a temperatura conforme a equação Neste processo, a temperatura do corpo variou de para . O calor recebido pelo corpo no processo é dado por

1. .
2. .
3. .
4. .
5. .
6. .

1. Os gráficos abaixo representam diferentes funções da energia de um gás . O gráfico que pode ser usado para representar adequadamente o comportamento da energia interna de de um gás ideal em função do produto da pressão pelo volume de gás é:

Um grande tanque aberto superiormente, com paredes verticais, contém um fluido ideal em repouso com profundidade . Um orifício, com dimensões muito menores que as do tanque, é aberto em uma das paredes verticais na profundidade , pelo qual o fluido escoa com velocidade na direção horizontal. Determine a distância horizontal percorrida pelo jato de corrente após sair do tanque até tocar na base de apoio do mesmo. Considere a velocidade do fluido na superfície superior do tanque desprezível.

1. .
2. 2h
3. 2
4. 2(H – h)
5. 2

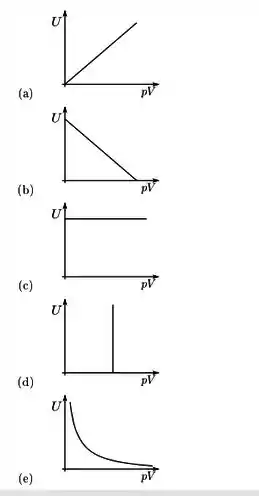
Um recipiente vedado, com a forma indicada na figura 1 é totalmente preenchido por um fluido ideal. As pressões em dois pontos do fluido neste recipiente são indicadas por (no ponto ) e (no ponto ). A figura 2 mostra um tubo que sofre estreitamento e pelo qual escoa (escoamento estacionário) um fluido ideal incompressível. As pressões em dois pontos do fluido neste tubo são indicadas por (no ponto) e (no ponto ). É correto afirmar:

.

1. .

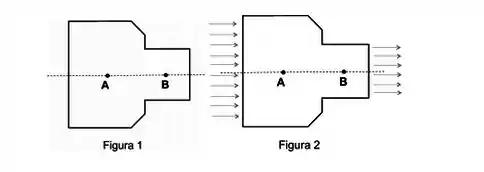
Sobre quatro balanças idênticas são colocados recipientes preenchidos por um mesmo líquido. O primeiro só contém o liquido; o segundo, um corpo flutuando em equilíbrio; o terceiro, um corpo totalmente submerso, que não flutua, pois está preso ao fundo por um fio tenso e o quarto um corpo que não afunda, pois está suspenso por um fio preso ao teto. Nestas situações as alturas das superfícies livres do líquido em todos os recipientes é a mesma, como mostra a figura. Sejam , , , as marcações da balança compara-se as:

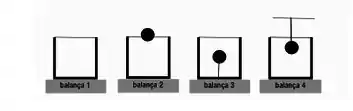
Três recipientes idênticos são preenchidos até uma mesma altura com dois líquidos imiscíveis e incompressíveis distintos de densidades e (). No primeiro, é colocado apenas o líquido de densidade ; no segundo, apenas o líquido de densidade e, no terceiro, uma mistura em partes iguais dos dois líquidos.

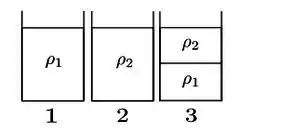
Em cada um dos recipientes, é colocado um mesmo objeto pequeno de densidade . Considere a altura dos líquidos em cada um dos recipientes após o objeto ser colocado. Compare:

a)

b)

c)

d)

e)

O gráfico X a seguir mostra como o volume de um mol de um gás ideal varia com a pressão ao longo de dois processos e .Sobre esses processos, é correto afirmar que

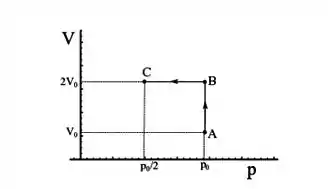
1. A variação da energia ao longo de todo o processo é nula.
2. O trabalho realizado pelo gás é nulo no processo .
3. No processo , o gás recebeu uma quantidade de calor equivalente a .
4. A variação de temperatura é negativa no processo .
5. No processo , o gás perde calor e uma quantidade positiva e não-nula de trabalho é realizada sobre ele.
6. A variação de entropia no processo é nula, pois o processo é reversível.

Considere que um mol de um gás ideal se expande até dobrar de volume isotermicamente a temperatura e outro mol do mesmo gás, também a temperatura , dobra de volume através de uma expansão livre. Sobre esses dois processos, são feitas as seguintes assertivas:

1. O trabalho realizado em ambos os processos pode ser calculado através da expressão , onde é a pressão do gás e , o seu volume.
2. A variação de entropia do gás é a mesma nos dois processos e é dada pela expressão .
3. O calor recebido pelo gás em ambos os processos pode ser calculado pela expressão .
4. A variação de entropia do gás nos dois processos é ; logo, ambos os pro essos são irreversíveis.
5. Em ambos os processos, o estado final atingido pelo gás é diferente do inicial; logo, a variação de energia interna do gás nos dois necessariamente deve obedecer .

São verdadeiras:

(a) Apenas I e II.

(b) Apenas a II.

(c) Apenas I, II e III.

(d) Apenas II e IV.

(e) Apenas a V.

(f ) Apenas III, IV e V.

(g) Apenas I, II e IV.

A figura abaixo mostra um trecho de um tubo de paredes rígidas por onde escoa um fluido incompressível, de densidade ρ, em regime estacionário. Despreze os efeitos da viscosidade do fluido. Seja a área da seção reta da parte esquerda do tubo e a área da seção reta da parte direita. A velocidade do fluido no ponto é 1. Considere conhecida a aceleração da gravidade. Responda:

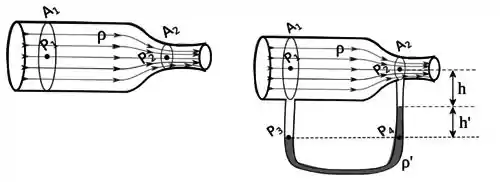
1. Qual a velocidade do fluido 2 no ponto P2? Escreva sua resposta em termos de 1, e .
2. b) Qual a diferença () das pressões do fluido, respectivamente, nos pontos P2 e P1? Escreva sua resposta em termos de 1, ρ, A1 e A2 .

É acoplado neste tudo, um pequeno tubo em (a figura está fora de escala), como indica a figura abaixo à direita, preenchido por um fluido também ideal e incompressível de densidade ρ′ a fim de que, medindo a altura ′ de desnível entre os dois braços deste tubo, seja possível encontrar a velocidade . A altura dos pontos P1 e P2 em relação ao desnível do fluido de densidade ρ′ é .

3. Encontre a pressão p3 no ponto P3 em função de p1 e a pressão p4 em P4 em função de p2 . Escreva suas respostas também em termos de ρ, ρ′ e ′.
4. Reobtenha a diferença () das pressões do fluido, respectivamente nos pontos P2 e P1, mas agora em termos de ρ, ρ′ e ′.
5. Determine a velocidade 1, em termos de ρ, ρ′ , ′ , A1 e A2. Considere a área da seção reta do tubo em desprezível quando comparada com A1 e A2 .
6. Qual deve ser o valor de ′ para que as pressões nos pontos P1 e P2 sejam iguais? O que acontece com o escoamento do fluido de densidade ρ neste caso?