Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
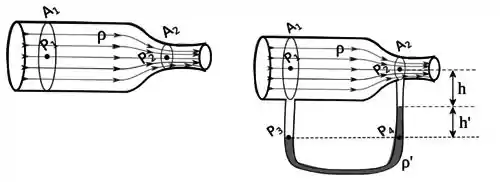
A figura abaixo mostra um trecho de um tubo de paredes rígidas por onde escoa um fluido incompressível, de densidade ρ, em regime estacionário. Despreze os efeitos da viscosidade do fluido. Seja a área da seção reta da parte esquerda do tubo e a área da seção reta da parte direita. A velocidade do fluido no ponto é 1. Considere conhecida a aceleração da gravidade. Responda:
- Qual a velocidade do fluido 2 no ponto P2? Escreva sua resposta em termos de 1, e .
- b) Qual a diferença () das pressões do fluido, respectivamente, nos pontos P2 e P1? Escreva sua resposta em termos de 1, ρ, A1 e A2 .
- Encontre a pressão p3 no ponto P3 em função de p1 e a pressão p4 em P4 em função de p2 . Escreva suas respostas também em termos de ρ, ρ′ e ′.
- Reobtenha a diferença () das pressões do fluido, respectivamente nos pontos P2 e P1, mas agora em termos de ρ, ρ′ e ′.
- Determine a velocidade 1, em termos de ρ, ρ′ , ′ , A1 e A2. Considere a área da seção reta do tubo em desprezível quando comparada com A1 e A2 .
- Qual deve ser o valor de ′ para que as pressões nos pontos P1 e P2 sejam iguais? O que acontece com o escoamento do fluido de densidade ρ neste caso?
É acoplado neste tudo, um pequeno tubo em (a figura está fora de escala), como indica a figura abaixo à direita, preenchido por um fluido também ideal e incompressível de densidade ρ′ a fim de que, medindo a altura ′ de desnível entre os dois braços deste tubo, seja possível encontrar a velocidade . A altura dos pontos P1 e P2 em relação ao desnível do fluido de densidade ρ′ é .
Passo 1
- :
- :
- :
- :
- :
- Pela a equação:
Basta a gente aplicar a equação da continuidade aqui:
Passo 2
Agora vamos aplicar Bernoulli entre os dois pontos, lembrando que as alturas são iguais. Assim, a equação ficará na forma:
Substituindo o valor de
Passo 3
Bom, como o ponto 3 está a uma profundidade em relação à , podemos escrever a pressão no ponto 3 como:
Podemos obter a pressão em de forma semelhante, a partir da profundidade do ponto 4 em relação ao ponto 2. Porém, preste atenção numa coisa nesse momento: A coluna de líquido, nesse caso, é composta por dois fluidos de densidades diferentes.
Assim:
Passo 4
Os pontos e estão na mesma altura, então podemos dizer, por Stevin, que eles possuem a mesma pressão. Assim:
Passo 5
Agora, determinado :
Passo 6
Se , teremos:
Nesse caso, o tubo de baixo não terá um desnível. Opa, mas o que isso quer dizer? Se não há um desnível, não existe diferença de pressão entre os pontos 1 e 2 no escoamento da parte de cima. Assim, analisando a diferença de pressão obtida pela a equação de Bernoulli:
Beleza?
Mas isso pode acontecer se realmente houver um escoamento? Claro que não! Como vimos, existe uma diferença entre as áreas dos pontos 1 e 2. Isso impossibilita que as duas velocidades, pelo princípio da continuidade, sejam iguais....a não ser que:
Nesse caso, o princípio da continuidade não é quebrado.
Resposta
- :
- :
- :
Não há escoamento