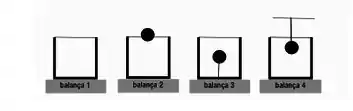
Sobre quatro balanças idênticas são colocados recipientes preenchidos por um mesmo líquido. O primeiro só contém o liquido; o segundo, um corpo flutuando em equilíbrio; o terceiro, um corpo totalmente submerso, que não flutua, pois está preso ao fundo por um fio tenso e o quarto um corpo que não afunda, pois está suspenso por um fio preso ao teto. Nestas situações as alturas das superfícies livres do líquido em todos os recipientes é a mesma, como mostra a figura. Sejam , , , as marcações da balança compara-se as:

2- Nesse caso, temos um corpo flutuando. Pelo princípio de Arquimedes, ou empuxo, sabemos que a massa de fluido deslocado é igual a massa do corpo que o desloca. Então, qual será a marcação da balança? Como o nível de líquido é o mesmo da primeira figura, a massa do líquido deslocado será exatamente igual a massa do corpo que está flutuando. Assim, o que jorrou de água pra fora do recipiente foi substituído pela massa do corpo, mantendo assim a massa total. Então:

3 - Opa! Temos uma corda ali dentro. Isso quer dizer que temos uma força agindo no corpo submerso. Porém, lembra de física 1? Se chamarmos o sistema de , percebemos que a força de tensão será uma força ao sistema. Uma força interna não afeta o sistema.

Agora nesse caso a densidade da bolinha é menor que a densidade do liquido, certo? Isso por que o fio está esticado! Assim o peso da bolinha é menor do que o peso do volume deslocado de água, assim a força medida pela balança é menor, ou seja

4- E nesse caso? Bom, agora a densidade da bolinha é maior do que a densidade do líquido. Como a bolinha tá toda afundada, a força que o a bolinha exerce sobre o fluido será a reação do empuxo, assim a normal causada pelo o líquido será exatamente igual a .

E o peso da bolinha não influencia? A tração desse fio de cima tá justamente compensando , fazendo com que a bolinha fique parada.

Assim,

Por fim: