Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação de Bernoulli

Ver Teoria
Exercício 57123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555658596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag

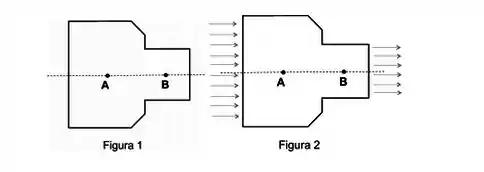
Um recipiente vedado, com a forma indicada na figura 1 é totalmente preenchido por um fluido ideal. As pressões em dois pontos do fluido neste recipiente são indicadas por p A (no ponto A ) e p B (no ponto B ). A figura 2 mostra um tubo que sofre estreitamento e pelo qual escoa (escoamento estacionário) um fluido ideal incompressível. As pressões em dois pontos do fluido neste tubo são indicadas por p ' A (no ponto A ) e p ' B (no ponto B ). É correto afirmar:

.

  1. . p A = p B ; p A ' < p B '
  2.   p A = p B ; p A ' = p B '
  3.   p A > p B ; p A ' = p B '
  4.   p A < p B ; p A ' = p B '
  5.   p A > p B ; p A ' < p B '
  6.   p A < p B ; p A ' < p B '
  7. p A = p B ; p A ' > p B '

Passo 1

Nessa questão, temos dois regimes diferentes: O estático, na figura 1, e o dinâmico, na figura 2.

Passo 2

Vamos analisar primeiro a figura 1:

Temos dois pontos na mesma altura. Isso te lembra o que? Isso ai, Stevin.

E por Stevin, sabemos que pressões em alturas iguais são iguais, assim:

p A = p B

Passo 3

Na figura 2, devemos pensar de outra forma. Como estamos levando em consideração um fluido em movimento, devemos utilizar a equação de Bernoulli:

ρ v A 2 2 + p A ' = ρ v B 2 2 + p B '

p B ' - p A ' = ρ 2 . v A 2 - v B 2

Bom, agora devemos analisar a continuidade: Como a área no trecho B é menor que a do trecho A , podemos dizer que:

A A v A = A B v B → v B = A A v A A B

Como A B < A A :

v B > v A

Passo 4

Logo, como : v B > v A

A diferença:

ρ 2 . v A 2 - v B 2 < 0

Será negativa.

Então, voltando pra primeira equação:

p B ' - p A ' < 0 → p B ' < p A '

Assim:

p A = p B

p A ' > p B '

g )

Resposta

g)

Exercícios de Livros Relacionados

O tubo de Pitot (veja a figura) é usado para medir a velocidade do ar nos aviões. Ele é formado por um tubo externo com pequenos furos B (quatro são mostrados na figura) que permitem a entrada de ar n
Na figura, a água entra em regime laminar no lado esquerdo de uma tubulação (raio r 1 = 2,00R ), atravessa a parte seção central (raio R ), e sai pelo lado direito (raio r 3 = 3,00R ). A velocidade da
As linhas de correntes horizontais em torno das asas de um pequeno avião são tais que a velocidade sobre a superfície superior é igual a 70,0m/s e sobre a superfície inferior é igual a 60,0m/s. Se a á
A figura mostra um jorro d’água saindo por um furo a uma distância h = 10c m da superfície de tanque que contém H = 40c m de água. (a) A que distância x a água atinge o solo? (b) A que profundidade de
A água se move com uma velocidade de 5,0m / s em um cano com uma área de seção reta de 4,0c m 2 . A água desce gradualmente 10 m enquanto a seção reta aumenta para 8,0c m 2 . (a) Qual é a velocidade d