Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Aplicações da Hidrodinâmica

Ver Teoria
Exercício 321234567891011121314151617181920212223242526272829303133343536373839404142434445464748

Enunciado

Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag

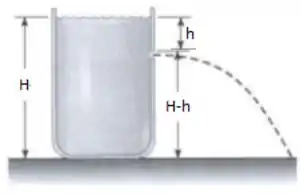
Um grande tanque aberto superiormente, com paredes verticais, contém um fluido ideal em repouso com profundidade H . Um orifício, com dimensões muito menores que as do tanque, é aberto em uma das paredes verticais na profundidade h , pelo qual o fluido escoa com velocidade na direção horizontal. Determine a distância horizontal percorrida pelo jato de corrente após sair do tanque até tocar na base de apoio do mesmo. Considere a velocidade do fluido na superfície superior do tanque desprezível.

  1. 2 H .
  2. 2h
  3. 2 h ( H - h )
  4. 2(H – h)
  5. 2 H ( H - h )

Passo 1

Isso é um caso de lançamento horizontal de um fluido. Como faremos isso? Vamos aplicar Bernoulli no ponto inicial, superfície do tanque, e no ponto final, ponto de saída do fluido.

Passo 2

Assim:

p 1 + ρ v 1 2 2 + ρ g h 1 = p 2 + ρ v 2 2 2 + ρ g h 2

Bom, como o tanque é aberto pra atmosfera, temos:

p 1 = p a t m

E como o orifício por onde o fluido passa também está aberto pra atmosfera:

p 2 = p a t m

A altura da superfície do tanque é H e altura do furo é H - h . Além disso, v 1 ≅ 0 .

Passo 3

Assim:

p a t m + 0 + ρ g H = p a t m + ρ g H - h + ρ v 2 2 2

∴

ρ v 2 2 2 = ρ g h → v 2 = 2 g h

Passo 4

Já temos a velocidade com a qual o fluido sai do tanque. Agora só precisamos lembrar que a distância horizontal é dada por:

d = v x ∆ t q u e d a

Como a velocidade é totalmente horizontal, temos:

v x = v 2

E o tempo de queda?

Bem, ele é dado por aquela velha formula de física1:

∆ t = 2 ∆ S g

A altura será a altura do furo:

∆ S = H - h

Assim

d = 2 g h . 2 H - h g = 2 g h . 2 H - h g = 4 h H - h = 2 h H - h

Então:

c)

Resposta

c)

Exercícios de Livros Relacionados

A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo A B C deve estar inicialmente cheio, mas, se essa condição é satisfeita, o líquido escoa pelo
Uma transição abrupta ocorre nos números de Reynolds de cerca de 3 * 10 5 , onde o arrasto em uma esfera se move através de um fluido diminui abruptamente. Estimar a velocidade com que essa transição
O cano de saída do esgoto de uma casa construída em uma encosta está a 6,59m abaixo do nível da rua. Se o cano coletor do esgoto está 2,16m abaixo do nível da rua, calcule a menor diferença de pressão
Qual é a área mínima (em metros quadrados) da supefície superior de uma placa retangular de gelo com 0,441m de espessura que flutua na água doce para que seja capaz de sustentar um automóvel de 938k g
A água flui através de um tubo horizontal de 25,0 cm de comprimento um diâmetro interno de 1,20 mm em 0,300 mL/s. Encontre a diferença de pressão necessária para conduzir esse fluxo se a viscosidade d