Três recipientes idênticos são preenchidos até uma mesma altura com dois líquidos imiscíveis e incompressíveis distintos de densidades e (). No primeiro, é colocado apenas o líquido de densidade ; no segundo, apenas o líquido de densidade e, no terceiro, uma mistura em partes iguais dos dois líquidos.
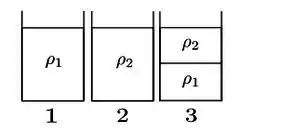
Em cada um dos recipientes, é colocado um mesmo objeto pequeno de densidade . Considere a altura dos líquidos em cada um dos recipientes após o objeto ser colocado. Compare:
a)
b)
c)
d)
e)
Passo 1
Vamos considerar que o objeto que está sendo colocado nos recipientes é um cubo, pra facilitar as contas, já que nesse caso, o volume submerso do cubo é dado por:
Onde é a área da base. E, por consequência disso, a altura que cada líquido passará a ter será dada por:
Onde seria a altura inicial do líquido. Sacou? Computaremos a altura que o corpo afundará será igual a altura que o fluido subirá.
Passo 2
Vamos analisar uma por uma:
1 - Nesse caso, pelo equilíbrio de forças, que leva a , teremos:
Passo 3
2 - Agora, repetindo o mesmo procedimento, teremos:
Comparação: Quem é maior, ou
Então quem é maior, ou Bom, como os serão inversamente proporcionais às densidades, podemos dizer que:
Passo 4
3- E agora? Temos dois líquidos, um em cima do outro. Como calcular isso? Bom, a primeira coisa que você precisa notar é que a densidade é menor que
Isso quer dizer que o corpo não afundará além desse fluido, portanto, o fluido de densidade não afetará a nossa conta.
E, por fim, o que isso diz? Diz que o cálculo será exatamente como no caso 2:
Passo 5
Então, teremos:
Isso é:
d)
Resposta
d)