P2 de Física 2 da UFRJ - 2017.2

Uma massa presa na extremidade de uma mola ideal oscila com amplitude A, obedecendo à lei de Hooke. A que distância da posição de equilíbrio está a massa, no instante em que as energias potencial e cinética são iguais?

a)

b)

c)

d)

e)

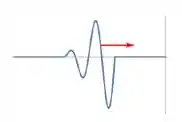
Considere um sistema massa-mola amortecido de massa m = 1 kg e constante de mola k = 1 N/m, cujo movimento é ilustrado pela figura abaixo:

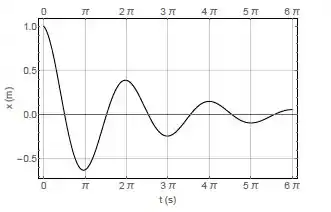
A respeito desse sistema é CORRETO afirmar:

(a) A frequência angular de oscilação é

(b) A constante de amortecimento é .

(c) A constante de amortecimento é .

(d) O sistema tinha inicialmente (t = 0) velocidade positiva.

(e) O sistema tinha inicialmente (t = 0) velocidade negativa.

Uma partícula de massa m se move horizontalmente em um plano sem atrito, com velocidade v0 e atinge uma mola com constante elástica k. Ao atingir a mola, esta é comprimida e a partícula é ricocheteada com velocidade oposta. Assumindo que não existe nenhuma perda de energia, o tempo em que a partícula permanece em contato com a mola e a compressão máxima sofrida pela mola, são dados respectivamente por:

a) e

b) e

c) e

d) e

e) Nenhuma das alternativas.

Considere as seguintes afirmações sobre oscilações forçadas amortecidas, quando a força é dada por F = F0 cos(t) e é a frequência natural das oscilações.

I. Para uma dada amplitude F0, a solução estacionária na frequência de ressonância pode ter amplitude no máximo igual a 4 vezes a amplitude de oscilação no limite .

II. Para , o sistema responde com uma baixa amplitude de oscilação.

III. No regime de amortecimento fraco e baixa frequência (), o movimento está em oposição de fase com a força externa.

Quais destas afirmações são corretas?

(a) Nenhuma.

(b) I, II e III.

(c) Apenas I e II.

(d) Apenas I e III.

(e) Apenas II e III.

(f) Apenas I.

(g) Apenas II.

(h) Apenas III.

Um estudante de física II foi assistir ao show do Guns and Roses no Rock in Rio. Ele estava se sentindo desconfortável com o barulho e usando um medidor de decibéis, verificou que o nível de intensidade do som atingia o limiar de sensação dolorosa de 120 db a uma distância d1 = 2 m do palco. Com o objetivo de aliviar o desconforto auditivo, o aluno resolveu se afastar a uma distância d2 do palco, até reduzir o nível de intensidade para 100 db. Sabendo que o limiar de audibilidade é , qual deveria ser a distância d2 do aluno em relação ao palco?

(a) d2 = 12 m

(b) d2 = 3 m

(c) d2 = 6 m

(d) Nenhuma da alternativas.

(e) d2 = 10 m

(f) d2 = 20 m

Dois alto-falantes transmitem o mesmo sinal harmônico, recebido em fase de um único oscilador. Os alto-falantes estão a uma distância de 6 m e 8 m, respectivamente, de um microfone que capta o som de ambos. Qual o menor comprimento de onda necessário para que haja interferência (i) completamente construtiva e (ii) completamente destrutiva?

(a) (i) 4 m e (ii) 2 m

(b) (i) 2 m e (ii) 8 m

(c) (i) 2 m e (ii) 4 m

(d) (i) 4 m e (ii) 1 m

(e) (i) 4 m e (ii) 2 m

Considere um oscilador harmônico simples, inicialmente na posição de equilíbrio, e as três condições abaixo:

I. (0) = 0;

II. (0) = v0;

III. (0) = 2v0.

Marque a alternativa correta:

(a) Em todos os casos o corpo ficará sempre parado, pois já está na posição de equilíbrio.

(b) O corpo atingirá o deslocamento máximo em menos tempo no caso III.

(c) O corpo oscilará com a mesma amplitude nos casos II e III.

(d) A energia mecânica total do oscilador no caso III é o dobro da do caso II.

(e) O corpo atingirá o deslocamento máximo ao mesmo tempo nos casos II e III.

Considere as seguintes funções y(x; t):

I. y(x; t) = 2

II. y(x; t) = cos (x) sin (t)+cos (4x) sin (4t)

III. y(x; t) = sin (5x - t) + 4 cos (5x - t)

IV. y(x; t) = 3 cos (2x) sin (10t)

Assinale a alternativa correta:

(a) I representa uma onda progressiva viajando da esquerda para direita.

(b) II não representa uma onda.

(c) III representa uma superposição de duas ondas estacionárias.

(d) IV representa uma onda estacionária.

Uma corda de um violino pode ser representada por uma corda presa nas duas extremidades de densidade linear e comprimento L. A velocidade de propagação de ondas transversais nessa corda é v.

(a) Encontre as frequências e os comprimentos de onda dos modos normais de vibração dessa corda do violino.

(b) Desenhe a forma da corda associada aos três modos de vibração mais baixos

(c) Mostre que os modos normais de vibração são descritos pela equação:

(d) Sabendo que um elemento da corda se move segundo um movimento harmônico simples, calcule a energia total de oscilação da corda, quando está vibrando no n-ésimo modo normal.

Uma onda é enviada por uma corda homogênea presa pela extremidade da direita. O perfil instantâneo da onda está ilustrado na figura abaixo.

Identifique o perfil instantâneo da mesma onda depois que ela se reflete na extremidade direita da corda.

a)

b)

c)

d)

e)