Uma corda de um violino pode ser representada por uma corda presa nas duas extremidades de densidade linear e comprimento L. A velocidade de propagação de ondas transversais nessa corda é v.
(a) Encontre as frequências e os comprimentos de onda dos modos normais de vibração dessa corda do violino.
(b) Desenhe a forma da corda associada aos três modos de vibração mais baixos
(c) Mostre que os modos normais de vibração são descritos pela equação:
(d) Sabendo que um elemento da corda se move segundo um movimento harmônico simples, calcule a energia total de oscilação da corda, quando está vibrando no n-ésimo modo normal.
Passo 1
a) Como as duas pontas da corda tão presas, o comprimento de onda fundamental vai ser:
A frequência fundamental vai ser:
As frequências dos modos seguintes são:
Como:
Então:
Passo 2
b) O desenho dos modos vai ficar assim:
Modo fundamental:
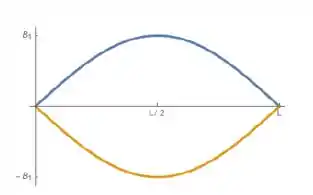
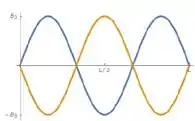
Segundo modo:
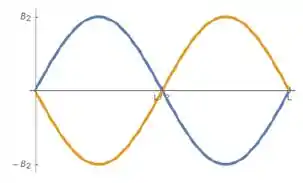
Terceiro modo:
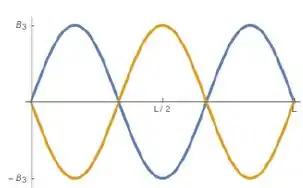
Passo 3
c) Para que as pontas da corda sejam fixas, a função precisa ter um termo:
Show. Nós sabemos que:
Então:
Reparou que se você trocar x por zero ou x por L o seno zera? Exatamente como queríamos.
Passo 4
Para descrever uma onda estacionária harmônica, precisamos de um termo da forma:
E como:
Os modos podem ter amplitude B e ângulo de fase , então:
Passo 5
d) Cada ponto da corda pode ser considerado uma partícula de massa dx que realiza um MHS de acordo com a equação de movimento da corda.
Tem uma fórmula pra energia de cada ponto da corda, no modo normal. Mas vamos ter que integrar! A fórmula é:
A velocidade v da corda a gente acha assim:
A frequência angular do modo n é:
Então:
Vamos integrar:
Fazendo uns cálculos muito lokos, a gente acha que essa integral aí é:
Então:
Resposta
a)
b) Modo fundamental:
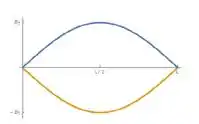
Segundo modo:
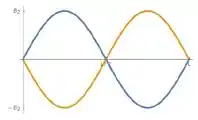
Terceiro modo:
c) Demonstração
d)