P3 de Física 2 da UFRJ - 2019.2

. Um gerador de frequências está acoplado a uma mola, cuja constante de rigidez é presa a um bloco de massa . Os sistema massa-mola por sua vez está preso a direita a uma corda de comprimento e massa . Para que o bloco não se desloque para direita uma outra corda é presa a ele pela esquerda (ver figura) e verifica-se que a tensão sobre ela é de .

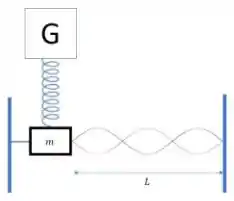
Considere que o amortecimento seja fraco e que depois de um certo tempo que o gerador de frequências está ligado se atinja o estado estacionário e a corda a direita esteja no terceiro modo de vibração cuja amplitude de deslocamento seja . A amplitude de oscilação do bloco é bem menor e o ponto de contato da corda com o bloco pode ser considerado um nó.

Com base nessas informações:

Determine o comprimento de onda da onda estacionária da corda a direita.

Determine a frequência de oscilação da corda e a do gerador de frequências.

Escreva a equação da onda estacionária da corda, dado que no instante os deslocamentos dos pontos da corda eram máximos. Não substitua o valor numérico de caso apareça.

. Um bloco está pendurado em uma mola, em repouso na posição de equilíbrio. Nesta situação a deformação da mola vale . O bloco é então puxado para baixo, alongando a mola, de mais , e abandonado a partir do repouso. Se necessário, use e deixe as respostas em termos de .

Determine a frequência angular e o período das oscilações subsequentes.

Determine a amplitude e a constante de fase da função que descreve o movimento do bloco. Escolha um eixo de coordenadas orientado verticalmente para cima, com origem no ponto onde o bloco está inicialmente em equilíbrio.

Determine a velocidade máxima alcançada pelo bloco.

Determine o instante em que pela primeira vez a energia cinética se iguala à energia potencial.

. Considere as seguintes afirmativas a respeito de um oscilador harmônico amortecido forçado:

. Uma vez atingido o regime estacionário, o trabalho médio da força externa resultante sobre o sistema é nulo.

. Quando o atrito sobre o oscilador é relativamente pequeno e a frequência da força externa sobre o oscilador harm��nico é igual a sua frequência natural a amplitude do movimento se anula.

. Quanto maior é a frequência da força externa sobre o oscilador, na média, mais energia por unidade de tempo é transferida ao sistema.

São VERDADEIRAS:

. Durante um processo adiabático reversível, podemos afirmar para a energia interna de um gás ideal monoatômico em função do volume que

é proporcional a

é proporcional a

é proporcional a

é proporcional a

. Uma corda de violino não está bem afinada, pois foi mais tensionada do que o necessário. Quando tocada ao lado de um diapasão (que vibra a ) pode-se ouvir quatro batimentos por segundo. Em qual frequência vibra a corda do violino?

. Uma moeda de ouro tem peso de módulo . Pesando-a novamente quando totalmente submersa em um fluido incompressível de densidade , seu peso aparente vale . Podemos então determinar a densidade da moeda como:

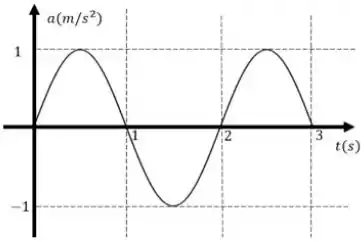
. Abaixo temos o gráfico da aceleração de um oscilador harmônico simples em função do tempo. A expressão que determina a posição, em metros, desse oscilador em função do tempo é

. Considere um tubo aberto de altura onde há uma onda sonora vibrando no modo fundamental. Se de alguma maneira aumentarmos , podemos afirmar que:

A frequência de oscilação diminui e o número de onda diminui.

O comprimento de onda aumenta e a velocidade da onda dentro da onda diminui.

O número de onda aumenta e o comprimento de onda aumenta.

A velocidade é a mesma e comprimento de onda é o mesmo.

A frequência aumenta e o comprimento de onda aumenta.

. Um carro anda com velocidade um décimo da velocidade do som em direção a um muro. Ao apertar a buzina, cujo som tem frequência , o som sai do carro bate no muro ecoando de volta no carro. A frequência do eco percebida por um passageiro do carro é dada por