. Um bloco está pendurado em uma mola, em repouso na posição de equilíbrio. Nesta situação a deformação da mola vale . O bloco é então puxado para baixo, alongando a mola, de mais , e abandonado a partir do repouso. Se necessário, use e deixe as respostas em termos de .
Determine a frequência angular e o período das oscilações subsequentes.
Determine a amplitude e a constante de fase da função que descreve o movimento do bloco. Escolha um eixo de coordenadas orientado verticalmente para cima, com origem no ponto onde o bloco está inicialmente em equilíbrio.
Determine a velocidade máxima alcançada pelo bloco.
Determine o instante em que pela primeira vez a energia cinética se iguala à energia potencial.
Passo 1
Vem comigo para mais essa!
Primeiro vamos ver a figura abaixo que representa nosso sistema.
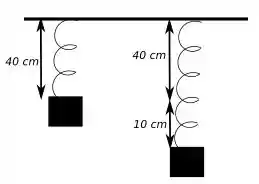
O do lado esquerdo representa o bloco antes de ser puxado e o da direita depois do bloco ser puxado.
No item para encontrar a frequência angular podemos usar a seguinte equação que nos fornece ela para uma mola pendura.
E o período podemos encontrar através da seguinte equação:
No item para encontrar o que ele quer vamos analisar a função da posição fornecida no instante inicial e vamos também encontrar a função da velocidade usando o fato de que:
Com isso vamos avaliá-las em já que (o valor é negativo, pois estamos usando a orientação de como sugerido pelo enunciado) e já que o bloco parte do repouso.
Na letra para achar a velocidade máxima vamos avaliar a função da velocidade que calculamos em e ver o valor que faz ela ser máxima.
O item quer que encontremos o instante em que .
Usando o fato de que:
Para isso vamos usar as expressões de do enunciado e a de que vamos calcular.
Mãos à obra!
Passo 2
Começando com o item .
Temos que a frequência angular é dada por:
Substituindo o que sabemos, temos:
Agora podemos achar o período de oscilação, temos:
Substituindo o valor de , ficamos com:
Passo 3
Agora vamos olhar o item .
Temos que a posição é dada por:
Olhando para , temos:
Precisamos do valor de que é a constante fase antes para acharmos . Para isso vamos olhar para a equação da velocidade.
Agora olhando para , temos:
Para isso ser verdadeiro temos que:
Mas como
e é positivo temos que deve ser negativo, logo . E com isso temos que:
Prontinho, mais um para conta.
Passo 4
Vamos achar o que o item quer.
Ele quer a velocidade máxima, temos que a velocidade é dada por:
Para ela ser máxima precisamos que o seno seja igual , logo:
O sinal não precisa ser levado em conta pois ele só diz em qual posição ele atinge a velocidade máxima ou em ou .
Substituindo os valores que conhecemos, temos:
Passo 5
Por último vamos resolver o item .
Temos que:
Substituindo com as equações da posição e da velocidade, temos:
Agora vamos usar uma outra definição de frequência angular que é:
Com isso temos:
Passo 6
Para continuarmos temos nos atentar que o enunciado quer o valor de para a primeira vez que essa igualdade acontece.
Só que isso acontece pela primeira vez entre o instante em que o bloco é solto e o instante que ele passa pelo ponto de repouso.
Nisso temos que a posição é negativa e a velocidade é positiva, para que isso acontece teremos que:
Mas isso só acontece quando para o seno e o cosseno de , então:
Usando que e , temos:
Com isso temos que: