. Um gerador de frequências está acoplado a uma mola, cuja constante de rigidez é presa a um bloco de massa . Os sistema massa-mola por sua vez está preso a direita a uma corda de comprimento e massa . Para que o bloco não se desloque para direita uma outra corda é presa a ele pela esquerda (ver figura) e verifica-se que a tensão sobre ela é de .
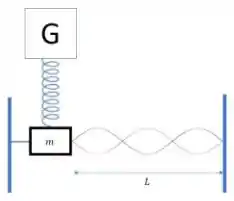
Considere que o amortecimento seja fraco e que depois de um certo tempo que o gerador de frequências está ligado se atinja o estado estacionário e a corda a direita esteja no terceiro modo de vibração cuja amplitude de deslocamento seja . A amplitude de oscilação do bloco é bem menor e o ponto de contato da corda com o bloco pode ser considerado um nó.
Com base nessas informações:
Determine o comprimento de onda da onda estacionária da corda a direita.
Determine a frequência de oscilação da corda e a do gerador de frequências.
Escreva a equação da onda estacionária da corda, dado que no instante os deslocamentos dos pontos da corda eram máximos. Não substitua o valor numérico de caso apareça.
Passo 1
Então vamos para mais uma! Esse problema se trata bem dizer uma onda estacionária em uma corda com massa.
Para determinar o comprimento de onda da onda estacionária podemos usar a seguinte equação:
Onde indica o modo de vibração que para esse caso é segundo enunciado.
Para determinar a frequência pedida em podemos usar o seguinte:
Já que a frequência do gerador é igual ao do bloco que é igual à da corda.
Onde acharemos no item e podemos achar com a seguinte relação:
Onde é a densidade linear da corda dada por .
E agora para achar a equação pedida em vamos usar o fato de que a equação de uma onda na forma mais geral é dada por:
Onde
Então basta calcularmos esses parâmetros para o caso da nossa corda e assim teremos a equação dela.
Passo 2
Vamos então começar a resolver esse problema, primeiro vamos lidar com o item . Temos o seguinte:
Usando que e , temos:
Passo 3
Agora vamos para o item .
Ele quer a frequência do gerador e da corda e para isso vamos usar:
Mas antes temos que calcular e para isso temos que calcular o valor de . Temos:
Usando o que sabemos, temos:
Agora podemos achar , temos:
Então temos que:
Finalmente podemos achar a frequência , temos:
Assim temos que:
Nos livramos de mais uma!
Passo 4
Agora vamos resolver o item .
Precisamos encontrar os parâmetros e . Vamos lá então.
Primeiro vamos encontrar , temos:
Vamos achar agora.
Para achar vamos usar o fato de que em temos o deslocamento máximo, assim:
Para isso ser máximo temos que para isso acontecer temos que .
Juntando tudo temos que nossa equação fica da seguinte forma:
Conseguirmos acabar com tudo!