UFRJ – Física 2 – 2019.2 – P3 – M. Escolha
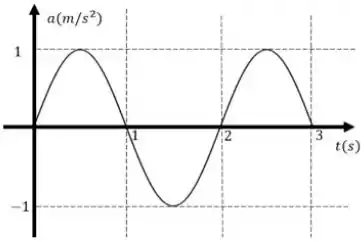
. Abaixo temos o gráfico da aceleração de um oscilador harmônico simples em função do tempo. A expressão que determina a posição, em metros, desse oscilador em função do tempo é
Passo 1
Vamos para mais esse problema e acabar com ele!
A equação da posição da forma mais geral possível é dada por:
Então temos que achar quem é e .
Para isso vamos analisar esse gráfico e usar a equação da aceleração que fornece esse gráfico, na sua forma mais geral, temos:
Com isso vamos analisar o gráfico e encontrar os parâmetros.
Passo 2
Primeiro, olhando o gráfico vemos que em temos que . Então:
Então temos que:
Passo 3
Analisando o gráfico mais um pouco temos que em temos aceleração máxima e para um oscilador temos que a primeira aceleração máxima é , então temos que:
Para que isso aconteça temos que:
Sabendo isso e que a aceleração máxima, olhando o gráfico, é , temos:
Passo 4
Agora juntando tudo isso temos que a equação da posição é dada por:
Agora se usarmos o fato de que a diferença de uma função cosseno para uma função seno é uma fase de , temos que:
E como seno é uma função ímpar, temos:
Logo a alternativa correta é a letra .