P1 de Física 2 da USP - 2017

Um bloco de massa M preso a uma mola de constante k descreve um movimento harmônico simples horizontal com uma amplitude . No instante em que o bloco passa pela posição de equilíbrio, um pedaço de massa m cai verticalmente sobre o bloco de uma pequena altura, grudando-se nele. A nova amplitude e período são:

(a)

(b)

(c)

(d)

(e)

Um móvel executa MHS e obedece à função horária , no SI. O tempo necessário para que este móvel vá da posição de equilíbrio para a posição de elongação máxima e o valor da aceleração no instante t são, respectivamente:

(a) 1 s e - cos(π/2t+π)

(b) 1 s e - π cos(2π/2t+2π)

(c) 2 s e - cos(π/2t+π)

(d) 1 s e - cos(3π/2t)

(e) 2 s e - /4 cos(π/2t+π)

Um planeta de massa m orbita uma estrela de massa M. Considerando a massa da estrela muito maior que a do planeta, podemos descrever a energia mecânica E do sistema (constante) em termos do momento angular L (constante), da distância entre o planeta e a estrela r e de sua velocidade radial :

Onde G é a constante gravitacional universal. Note que a contribuição da velocidade angular para a energia cinética é completamente descrita em termos do momento angular L e do momento de inércia I = mr2. A combinação desse termo com a energia potencial gravitacional dá origem a um potencial efetivo, Ue(r), dependente apenas de r.

(a) [1,0] Qual a distância re, correspondente ao mínimo da energia potencial efetiva?

(b) [1,0] Escreva a equação diferencial do movimento para pequenas oscilações ao redor de re, em termos de r’ = r - re.

(c) [1,0] Calcule a frequência de oscilação ao redor de re.

Dê suas respostas em termos de M, m, L, G.

Um corpo efetua um movimento harmônico simples linear (MHS), quando numa trajetória retilínea, oscila periodicamente em torno de sua posição de equilíbrio sob ação da força restauradora cuja intensidade é proporcional à distância do corpo ao ponto de equilíbrio. A figura ilustra um corpo de massa m preso a uma mola de constante elástica k que será abandonado da posição x= 2m para dar início ao MHS em torno da posição de equilíbrio x=0, com freqüência angular de 1 rad/s.

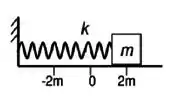
Despreza-se qualquer tipo de atrito ao movimento do corpo. Indique o gráfico que representa a função horária da velocidade do corpo de massa m em um período completo (T) de oscilação.

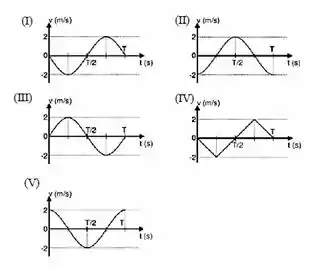
(a) Figura (I)

(b) Figura (II)

(c) Figura (III)

(d) Figura (IV)

(e) Figura (V)

Levando em consideração a oscilação na direção vertical de um carro, podemos considerar que este seja suportado por quatro molas idênticas. As molas de um carro são ajustadas de um certo modo que a frequência de vibração seja 4, 00Hz. Qual é a constante de cada mola se a massa do carro é 1500 kg e o peso é distribuído igualmente sobre as molas? Qual será a frequência de vibração se cinco passageiros, com 70 kg cada, ocupam o carro? (Considere )

(a) k = 2, 4 N/m e f = 3, 6Hz

(b) k = 9, 6 N/m e f = 3, 6Hz

(c) k = 2, 4 N/m e f = 1, 8Hz

(d) k = 9, 6 N/m e f = 1, 8Hz

(e) k = 9, 6 N/m e f = 1, 6Hz

Um pêndulo simples é constituído de uma massa de m = 1 kg suspensa por um fio de comprimento L com massa desprezível.

(a) [1,0] Escreva as equações de movimento para um ângulo de desvio em relação à posição de equilíbrio, justificando sua resposta. Supondo que o pêndulo execute pequenas oscilações em torno da posição de equilíbrio:

(b) [1,0] Determine o comprimento para que o período de oscilação seja de s.

(c) [1,0] Mostre que a energia total do pêndulo é constante.