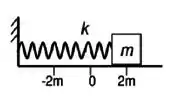
Um corpo efetua um movimento harmônico simples linear (MHS), quando numa trajetória retilínea, oscila periodicamente em torno de sua posição de equilíbrio sob ação da força restauradora cuja intensidade é proporcional à distância do corpo ao ponto de equilíbrio. A figura ilustra um corpo de massa m preso a uma mola de constante elástica k que será abandonado da posição x= 2m para dar início ao MHS em torno da posição de equilíbrio x=0, com freqüência angular de 1 rad/s.
Despreza-se qualquer tipo de atrito ao movimento do corpo. Indique o gráfico que representa a função horária da velocidade do corpo de massa m em um período completo (T) de oscilação.
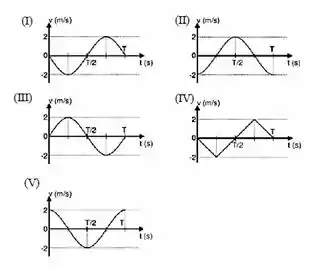
(a) Figura (I)
(b) Figura (II)
(c) Figura (III)
(d) Figura (IV)
(e) Figura (V)
Passo 1
Bom, se o corpo é abandonado da posição x = 2 m e oscila em torno da posição x = 0, podemos dizer que a amplitude do movimento é igual a 2 m.
O problema também diz que a frequência angular é de 1 rad/s. Então podemos escrever a função horária do cara, se compararmos com a forma geral:
Sabendo que é a frequência angular e A é a amplitude, fica:
Você pode se perguntar por que eu usei seno e não cosseno. Bem, se o corpo começa o movimento na posição x = 2 m, eu preciso que x(0) seja igual a 2. Se usar seno, isso não rola.
Passo 2
Agora que já temos a função horária do movimento, é só derivar uma vez pra achar a velocidade:
Show! Agora vamos ver qual dos gráficos é o desse cara. Repara que ali nas respostas em vez de ele colocar o valor do período, colocou T. Isso não faz diferença nenhuma pra gente porque poderíamos calcular o período simplesmente substituindo na fórmula:
Lembrando que a função seno começa em zero, depois vai pra 1, depois pra zero de novo, depois -1, depois pra zero de novo. Mas esse sinal de menos aí vai inverter a ordem desses números, então vai ser: zero, -1, zero, 1, zero de novo. Tudo isso multiplicado por 2! O gráfico mais parecido então vai ser o da letra A.
Resposta
Letra A