P1 de Física 2 da USP - 2018

Um pêndulo simples tem comprimento L e período natural de pequenas oscilações T. Quando ele passa por sua posição de equilíbrio, a corda é repentinamente presa no seu ponto médio. O período então torna-se:

1. Nenhuma das alternativas
2. T/2
3. 2T
4. T/4
5. T

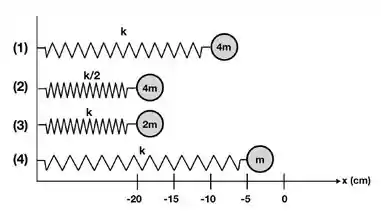
Quatro (4) molas de mesmo comprimento são comprimidas em relação à sua posição de equilíbrio como na figura. Qual resultado é satisfeito por suas velocidades máximas se as molas são liberadas a partir do repouso?

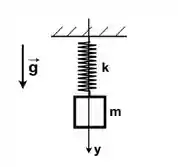
No sistema massa-mola com mola de constante de elasticidade da figura, se a massa é substituída por , qual é o efeito sobre a posição de equilíbrio (medida ao longo do eixo e a partir da extremidade da mola relaxada) e sobre o período?

1. A posição de equilíbrio será um fator menor e o período será um fator menor.
2. A posição de equilíbrio será um fator 2 menor e o período será um fator menor.
3. A posição de equilíbrio será um fator 2 maior e o período será um fator maior.
4. A posição de equilíbrio será um fator menor e o período será um fator maior.
5. A posição de equilíbrio será um fator menor e o período será um fator 2 maior.

As figuras (1), (2) e (3) mostram diferentes configurações de sistemas massa-mola. Todas as massas e molas das figuras são iguais. Em relação às frequências de oscilação, podemos afirmar que:

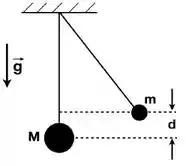
Duas massas, e , suspensas por fios de massas desprezíveis, de mesmo comprimento , são localizadas como mostrado na figura. A massa é solta e colide inelasticamente grudando em .

1. Calcule a velocidade de m imediatamente antes da colisão. Calcule a velocidade do conjunto formado por m e M imediatamente após da colisão.
2. Calcule a altura h máxima atingida pelo pêndulo formado por m e M.
3. Calcule a frequência natural e a amplitude para pequenas oscilações do sistema.

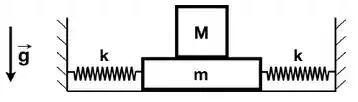
Uma plataforma de massa m está presa a duas molas iguais e de constantes elásticas k numa superfície horizontal sem atrito. Um bloco de massa M = 4m é colocado sobre a plataforma com as molas nas condições relaxadas, como mostrado na figura. Em função de k, m e M, responda:

1. Qual a frequência angular de oscilações dos blocos, quando estes são deslocados da posição de equilíbrio e liberados?
2. Calcule a amplitude máxima de oscilação para que o bloco não deslize sobre a plataforma, sabendo que o coeficiente de atrito estático entre o bloco e a plataforma é .
3. Soltando o bloco+plataforma de uma posição ( e com velocidade nula, determine a posição do sistema em função do tempo.