Uma plataforma de massa m está presa a duas molas iguais e de constantes elásticas k numa superfície horizontal sem atrito. Um bloco de massa M = 4m é colocado sobre a plataforma com as molas nas condições relaxadas, como mostrado na figura. Em função de k, m e M, responda:
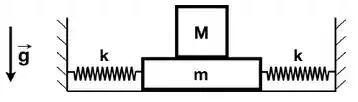
- Qual a frequência angular de oscilações dos blocos, quando estes são deslocados da posição de equilíbrio e liberados?
- Calcule a amplitude máxima de oscilação para que o bloco não deslize sobre a plataforma, sabendo que o coeficiente de atrito estático entre o bloco e a plataforma é .
- Soltando o bloco+plataforma de uma posição ( e com velocidade nula, determine a posição do sistema em função do tempo.
Passo 1
A) A figura a seguir mostra o diagrama de forças para o sistema de dois blocos quando este é deslocado de uma quantidade ao longo do eixo com respeito àquela posição em que as molas estão relaxadas.
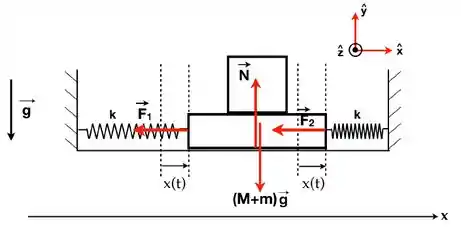
A força resultante sobre o sistema é então
de modo que a aplicação da segunda lei de Newton leva à equação de MHS para
com a frequência angular natural de oscilação dada por
Passo 2
B) O diagrama de forças para o corpo de massa encontra-se a seguir:
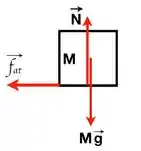
Enquanto os corpos oscilam conjuntamente, não há movimento relativo entre os blocos e, portanto, a força de atrito é do tipo estática. Na iminência do movimento entre os blocos, a força de atrito estático tem magnitude máxima igual a , de forma que a aceleração deste bloco também tem magnitude máxima A aceleração do bloco de massa , também pode ser escrita em termos do MHS realizado pelo conjunto
onde é apenas uma distância constante entre, por exemplo, o CM do bloco de massa e a extremidade de uma das molas. Do item anterior, a solução MHS para o movimento permite escrever
de modo que a magnitude máxima da aceleração do bloco é
Passo 3
C) Da solução geral aplicando as condições iniciais:
e
Temos que , logo:
Resposta
Ei, a resposta está no passo a passo :)