Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Pêndulo de Torção

Ver Teoria
Exercício 8123456791011

Enunciado

Duas massas, m e M , suspensas por fios de massas desprezíveis, de mesmo comprimento L , são localizadas como mostrado na figura. A massa m é solta e colide inelasticamente grudando em M .

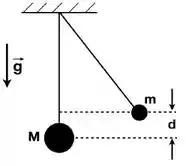
  1. Calcule a velocidade de m imediatamente antes da colisão. Calcule a velocidade do conjunto formado por m e M imediatamente após da colisão.
  2. Calcule a altura h máxima atingida pelo pêndulo formado por m e M.
  3. Calcule a frequência natural e a amplitude para pequenas oscilações do sistema.

Passo 1

A) A figura a seguir mostra os diagramas de forças para os corpos de massa m   e   M antes da colisão.

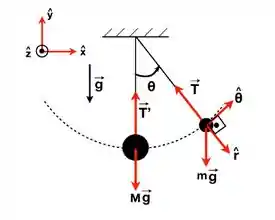
Sobre o corpo de massa m agem as forças peso m g e a tração T   no fio. Usando o teorema do trabalho-energia cinética, o trabalho da força resultante entre o ponto inicial e o ponto mais baixo da trajetória é igual à variação da energia cinética do corpo de massa m no mesmo percurso:

W = W g + W T = ∫ m g . d r + ∫ T . d r = - m g ∫ d 0 d y = m g d ,

onde usou-se o fato de que a tração T é perpendicular ao deslocamento durante toda a trajetória. A origem do sistema de coordenadas também foi tomada como estando no ponto mais baixo da trajetória. Logo

w = m g d = ∆ K = k f - K i = k f = 1 2 m v 2

v = 2 g d = - 2 g d

É claro do diagrama de forças que o sistema formado pelas duas massas não está isolado de forças externas. Logo, seu momento linear total não se conserva. Entretanto, imediatamente antes e imediatamente após a colisão, as velocidades estão essencialmente ao longo do eixo x e nesse curto intervalo de tempo, a força resultando ao longo do eixo x pode ser tomada como nula. Logo, temos para a componente x do momento linear:

- m 2 g d = M + m V

V = - m M + m 2 g d

Passo 2

B) Usando novamente o teorema do trabalho-energia cinética, agora para o sistema de duas massas unidas e entre o ponto mais baixo da trajetória e o ponto a altura h , temos novamente ( W   =   Δ K )

W = W g + W T = W g = - M + m g h

∆ k = K f - K i = - K i = - 1 2 M + m V 2 = - 1 2 M + m m M + m 2 2 g d

Logo

h = m M + m 2 d

Passo 3

C) Após a colisão, o sistema de duas massas forma um pêndulo simples de comprimento L e massa M + m. O ângulo q que o fio faz com a direção vertical, no limite de pequenas oscilações (q 1), satisfaz uma equação diferencial de oscilador harmônico simples

θ ˙ ˙ + ω 2 θ = 0 ,

onde, neste caso em particular, a frequência natural de oscilação é dada por 

ω = g L .

A solução da eq. diferencial em questão é

θ t = θ max ⁡ c o s ⁡ ( ω t + ϕ )

onde o ângulo máximo θ max ⁡ pode ser obtido a partir da altura h calculada no ítem anterior e do comprimento L do fio por

c o s θ max ⁡ = L - h L

θ max ⁡ = acos ⁡ 1 - h L

θ max ⁡ = acos ⁡ 1 - m M + m 2 d L .  

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

O balanço de um relógio antigo oscila com uma amplitude angular de πrad e um período de 0,500 s . Determine (a) a velocidade angular máxima do balanço, (b) a velocidade angular no instante em que o de
35. Um relógio da quatro tiques a cada segundo; cada tique corresponde à metade do período. A roda catarina do relógio consiste em uma fina camada circular com raio de 0,55c m conectada ao conjunto da
52.Um macaco mecânico de 1,80k g é suspenso por um pivô localizado a uma distância de 0,250m de seu centro de massa e começa a oscilar como um pêndulo físico. O período da oscilação com ângulo pequeno
13.6E Considere o pêndulo de torção mostrado na Figura 13.5 do texto. O disco tem massa de 200g e raio de 10,0cm . A constante de torção da barra vale 3,00 × 10 - 2Nm . Qual é o período de oscilação d
13.7E Reconsiderando o pêndulo do Exercício 13.6. A) qual é sua energia mecânica se no instante em que o ângulo de torção é θ = 5,00 ° sua velocidade angular é 0,600rad/s ?