P2 de Física 2 da USP - 2012

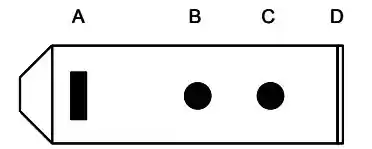
Uma flauta muito simples, como esquematizada na figura abaixo, possui sua extremidade aberta em Existe uma abertura em ( perto da parte que vai à boca) e também dois outros buracos em e A distância é igual a A distância do segmento é idêntica a do segmento Além disso, o segmento . Considere a velocidade do som no ar igual a . Qual seria a frequência do modo fundamental que você esperaria ouvir ao:

1. Assoprar, mantendo os buracos e fechados? Justifique a sua resposta.
2. Assoprar, tapando apenas o buraco Observa-se apenas que a variação de pressão entre os pontos e é basicamente nula. Justifique a sua resposta.
3. Assoprar, sem tapar os buracos e Justifique a sua resposta.
4. Considere que um amigo seu trouxe uma flauta parecida com a sua, mas que possui um comprimento diferente. Você e seu amigo começam a tocar suas flautas tapando os buracos e de suas respectivas flautas. Os sons emitidos por essa outra flauta lhe parecem ser mais agudos que aqueles produzidos pela sua flauta. Qual o comprimento total da flauta que seu amigo está tocando uma vez que você consegue medir com precisão (usando um aparelho) uma diferença de tom igual a

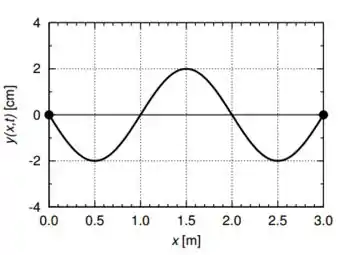
Em um sistema de coordenadas, uma corda homogênea de massa e extremidades fixas em e vibra em seu terceiro harmônico com amplitude máxima de acordo com:

Com dados em metros e em segundos. A figura ao lado mostra a configuração da corda no instante , com o eixo em metros e o eixo em centímetros. Após , observa-se que a corda passa instantaneamente pela primeira vez na configuração de equilíbrio, ou seja, para todo

1. Obtenha a velocidade de propagação de ondas na corda.
2. Obtenha a tensão na corda.
3. Obtenha a forma explícita de considerando e como funções co-seno.
4. Calcule as amplitudes e as constantes de fase ( das ondas progressivas e regressiva que, somadas, resultam na onda estacionária acima.

Dica: escreva , e , onde estão associadas as partes espacial e temporal de respectivamente.

Uma linha inteira carros Tabajara saiu com defeito de fabricação, emitindo um ruído harmônico de baixa frequência de e amplitudes idênticas. Um motorista em um carro silencioso e sem defeito viajava tranquilamente em uma estrada deserta e retilínea com velocidade quando de repente, à sua frente, dois carros Tabajara aparecem, um na mesma pista do motorista com e outro na pista contrária com velocidade (tanto como são dados em módulo). A estrada situa-se em uma região onde a velocidade do som é de

1. Calcule a frequência do ruído que chega ao motorista vindo do carro Tabajara.
2. Calcule a frequência do ruído que chega ao motorista vindo do carro Tabajara antes que esses carros se cruzem.
3. Calcule a frequência do ruído que chega ao motorista vindo do carro Tabajara após esses carros se cruzarem.
4. Calcule a frequência e o período do batimento do ruído resultante ouvido pelo motorista ainda antes dos carros e se cruzarem. Justifique, fazendo um esboço deste ruído em função do tempo.

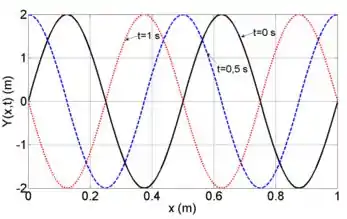
Na figura ao lado, são mostradas três instantes de tempos diferentes ( ) da função que descreve uma onda harmônica propagando-se em uma corda no sentido negativo de

Com base nas informações do gráfico:

1. Calcule o comprimento de onda, o período e a velocidade da onda ( Justifique).
2. Se a tensão na corda é , calcule a densidade linear de massa da corda.
3. Escreva a expressão para o perfil da onda
4. Calcule a velocidade e a aceleração transversais máximas de um elemento da corda.
5. Calcule a intensidade (ou seja, a potência média) da onda na corda.