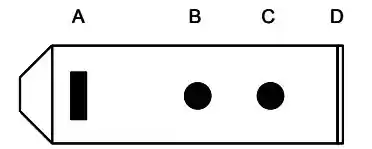
Uma flauta muito simples, como esquematizada na figura abaixo, possui sua extremidade aberta em Existe uma abertura em ( perto da parte que vai à boca) e também dois outros buracos em e A distância é igual a A distância do segmento é idêntica a do segmento Além disso, o segmento . Considere a velocidade do som no ar igual a . Qual seria a frequência do modo fundamental que você esperaria ouvir ao:
- Assoprar, mantendo os buracos e fechados? Justifique a sua resposta.
- Assoprar, tapando apenas o buraco Observa-se apenas que a variação de pressão entre os pontos e é basicamente nula. Justifique a sua resposta.
- Assoprar, sem tapar os buracos e Justifique a sua resposta.
- Considere que um amigo seu trouxe uma flauta parecida com a sua, mas que possui um comprimento diferente. Você e seu amigo começam a tocar suas flautas tapando os buracos e de suas respectivas flautas. Os sons emitidos por essa outra flauta lhe parecem ser mais agudos que aqueles produzidos pela sua flauta. Qual o comprimento total da flauta que seu amigo está tocando uma vez que você consegue medir com precisão (usando um aparelho) uma diferença de tom igual a
Passo 1
a):
Quando tapamos os buracos e , o tubo sonoro formado pela flauta passa a ter como seu comprimento efetivo o seu comprimento total:
Como a flauta é um tubo aberto, vamos usar a fórmula:
Então a frequência do primeiro harmônico será:
Passo 2
b):
Quando tapamos o buraco , o tubo sonoro efetivo passa a ter comprimento . Isso é, o ar entra por e sai por . Como é uma abertura pra atmosfera, e pressão atmosférica não muda, ali existe um nó de pressão, ou seja, um ponto de pressão invariável.
Então, calculando como fizemos em a), a frequência do primeiro harmônico será:
Passo 3
c):
Bom, você deve ter percebido que o ar sempre entra por , mas sempre sai pelo primeiro buraco que encontra pela frente. Quando deixamos os dois buracos abertos, o primeiro buraco que o ar encontra pra sair é o . Então o comprimento efetivo do tubo, nesse caso, vai ser
Passo 4
d):
Diferença de tom, nesse contexto, nos lembra o fenômeno do batimento.Bom, a frequência do batimento é dada por:
Como a segunda flauta gera sons mais agudos, a sua frequência fundamental deve ser maior que a da primeira flauta. Então, vamos chamar de a frequência da segunda flauta. Então:
Beleza! Muito simples agora, basta a gente usar a fórmula das frequências:
Resposta
a):
b):
c):
d):