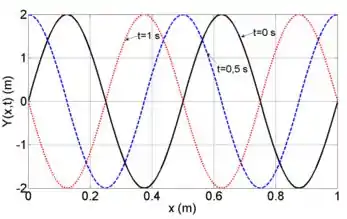
Na figura ao lado, são mostradas três instantes de tempos diferentes ( ) da função que descreve uma onda harmônica propagando-se em uma corda no sentido negativo de

Com base nas informações do gráfico:

1. Calcule o comprimento de onda, o período e a velocidade da onda ( Justifique).
2. Se a tensão na corda é , calcule a densidade linear de massa da corda.
3. Escreva a expressão para o perfil da onda
4. Calcule a velocidade e a aceleração transversais máximas de um elemento da corda.
5. Calcule a intensidade (ou seja, a potência média) da onda na corda.

b):

Opa, aqui é só usar aquela equação:

c):

Galera, a forma geral da equação de uma onda que se propaga na direção negativa de é:

Bom, por causa do período e do comprimento que já sabemos, fica fácil descobrir e

Agora precisamos achar . Podemos pegar o valor de quando

A gente viu que dá zero olhando no gráfico. Também pelo gráfico, dá pra perceber que a amplitude é:

Mas ainda não sabemos o valor da fase. Vamos derivara função em relação à e aplica-la no ponto

Pronto! Como a gente sabe que no ponto o valor dessa derivada é maior que zero? Basta olhar a tangente à curva quando (No caso, será a curva preta). Essa derivada sempre representa essa tangente se o gráfico for .

Então, juntando as informações:

d):

A velocidade transversal de um elemento da corda é sempre a derivada da função de onda em relação ao tempo:

O máximo da função ocorre pra , então:

E a aceleração é a derivada da velocidade em relação ao tempo:

O máximo também ocorre pra , então, a aceleração máxima em módulo é:

e):

A intensidade de uma onda é dada por:

Então: