Em um sistema de coordenadas, uma corda homogênea de massa e extremidades fixas em e vibra em seu terceiro harmônico com amplitude máxima de acordo com:
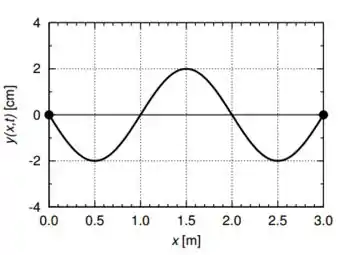
Com dados em metros e em segundos. A figura ao lado mostra a configuração da corda no instante , com o eixo em metros e o eixo em centímetros. Após , observa-se que a corda passa instantaneamente pela primeira vez na configuração de equilíbrio, ou seja, para todo
- Obtenha a velocidade de propagação de ondas na corda.
- Obtenha a tensão na corda.
- Obtenha a forma explícita de considerando e como funções co-seno.
- Calcule as amplitudes e as constantes de fase ( das ondas progressivas e regressiva que, somadas, resultam na onda estacionária acima.
Dica: escreva , e , onde estão associadas as partes espacial e temporal de respectivamente.
Passo 1
a):
A gente quer saber a velocidade de propagação da onda. Mas por onde começar? Bom, podemos pensar na seguinte relação abaixo:
Mas sendo o número de onda, sabemos que ele pode ser calculado por:
Beleza, mas estamos falando de harmônicos...como os harmônicos variam o comprimento de onda?(
Então vai ser:
Show! O harmônico da questão é o terceiro, logo:
Note que o valor do comprimento é e podemos ver isso no gráfico.
Pra descobrir a frequência angular , basta perceber que em os pulsos tem deslocamento máximo, como a gente pode ver pelo gráfico. Já em a onda era .
Uma ida do máximo ao zero corresponde a um deslocamento angular de basta você lembrar de uma função seno ou cosseno. Então:
Com os valores de e :
Passo 2
b):
Nós queremos a tensão da corda. Então a gente pode usar a equação:
A gente já tem e . Como temos o comprimento e a massa da corda, vale:
Substituindo na equação de cima:
Passo 3
c):
A função escrita em termos de funções cosseno, por ser uma onda estacionária, é escrita como:
Vamos descobrir o valor das fases usando condições iniciais. Sabemos que:
Como nessa condição nós alteramos o valor de ,devemos analisar o primeiro cosseno. A primeira condição nos diz que:
Pra descobrir o sinal da parada é só a gente perceber que no intervalo: o valor de , isso é, , já que temos uma função cosseno.
Então, resolvendo essa inequação ai pros valores de extremos:
Então :
E ? Bom, pra a gente percebe que a função tem seus máximos, então:
Então a função em sua forma explícita será:
A amplitude a gente consegue descobrir visualmente:
Passo 4
d):
Vamos escrever de novo as equações das ondas:
Chamando e :
E para , nós vamos fazer a mesma coisa:
Então somando todo mundo:
Ufa! Tá quase chegando ao fim. Mas olha só, pela equação que achamos no item anterior, c), não havia nenhum seno na equação. Então, o segundo termo da expressão acima tem que ser nulo, isso é:
Além disso, sabemos que a amplitude total vale
Vamos comparar as outras expressões:
Então, :
Perceba que uma de desloca no sentido de positivo,(a que tem o sinal de na frequência angular) e a outra no sentido de negativo( a que tem o sinal de na frequência angular).
Resposta
a):
b):
c):
d):