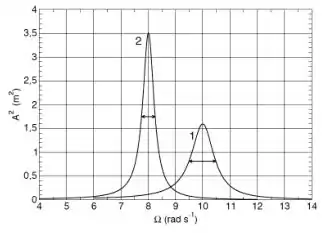
Um grupo de estudantes construiu um oscilador utilizando um bloco de massa e uma mola de constante elástica k. Um segundo grupo de estudantes construiu um outro oscilador acoplando um bloco de massa a uma mola idêntica àquela utilizada pelo primeiro grupo de estudantes. Os dois sistemas oscilam em um meio cuja força de resistência é proporcional à velocidade com o mesmo coeficiente de resistência . Cada grupo de estudantes aplicou uma força externa periódica de mesma amplitude aos sistemas. No regime estacionário, os valores máximos das potências médias dissipadas pelos osciladores em cada ciclo de oscilação, são dadas por e . Analisando a curva de ressonância abaixo, pode-se afirmar que:
(a) .
(b) .
(c) .
(d) .
(e) .
Passo 1
Temos aqui oscilações forçadas e amortecidas, com as forças elástica, amortecimento, e externa:
Juntando tudo na segunda lei de Newton
Substituindo e , dividindo tudo por m e reorganizando, temos que:
Definido a constante de amortecimento , a frequência natural de oscilação , temos a equação diferencial:
Onde vamos ter uma solução homogênea, que vai ser crítico, subcrítico ou supercrítico, todas decaem exponencialmente no tempo, que vão ser soluções transientes. E vamos ter uma solução particular, que vai ser a única que vai restar no regime estacionário.
Como estamos lidando apenas com a regime estacionário, vamos calcular apenas a solução particular, que vai ser:
Onde a amplitude é:
Passo 2
Na frequência de ressonância, quando a amplitude é máxima, ,
Como no gráfico temos , usando o fato que e que :
Comparando as amplitudes de 1 e de 2,
Como o meio é o mesmo e a mola é a mesma (), então:
Passo 3
Usando o fato que
Como os meios são iguais,
Como , então:
Passo 4
A potência média dissipada pode ser obtida pela expressão (não precisa se desesperar ela vai estar no formulário da prova):
A potência será máxima justamente na ressonância, quando , então:
Como vimos antes, a amplitude na ressonância é
E como :
Passo 5
Vamos comparar as potências para a curva 1 e curva 2
Vamos olhar no gráfico para ver quem o maior produto frequência-amplitude na ressonância.
Para a curva 1,
Na curva 2,
Então,
Podemos elevar ao quadrado dos dois lados para facilitar as contas:
Resposta
(d) .