P3 de Física 2 da USP - 2017

Um pulso que se propaga com velocidade de v = 40 m/s numa corda de comprimento com a extremidade x = L fixa é descrito pela função , onde = 10 cm e b = 4, 0 . A função que representa o pulso refletido em um instante t logo após sua primeira reflexão em x = L é:

a)

b)

c)

d)

e)

Marina e Fernando se movimentam com velocidades em relação a um observador inercial e estão escutando ondas sonoras produzidas por uma fonte de freqüência que se movimenta com velocidade ⃗ em relação ao mesmo observador, como mostrado na figura. Para as freqüências das ondas sonoras que Marina e Fernando escutam, pode-se dizer:

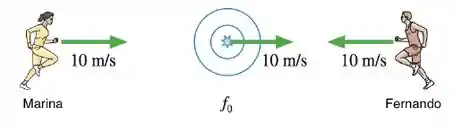
a) , onde e .

b) , onde e .

c) , onde e .

d) , onde e .

e) , onde e .

Uma onda estacionária em uma corda vibra como mostrado na figura. Se, nesse modo de vibração, T e L são, respetivamente, a tensão e o comprimento da corda e f é a frequência de vibração, pode-se dizer que:

a) Se , e , a corda vibra seguindo o modo mostrado na figura d.

b) Se , mantendo L e f, a corda vibra seguindo o modo mostrado na figura b.

c) Se e , mantendo f, a corda vibra seguindo o modo mostrado na figura c.

d) Se , mantendo L e f, a corda vibra seguindo o modo mostrado na figura a.

e) Nenhum dos modos de vibração mostrados nas figuras de (a) a (d) pode-se obter mudando T e/ou L e/ou f .

Marcelo e Edivaldo seguram pelas extremidades uma corda de comprimento L e densidade linear , aplicando uma tensão T. Ao movimentar as extremidades, eles geram ondas harmônicas progressivas em cada extremidade, de forma a obter ao final uma onda estacionária na corda, com os ventres nas posições de Marcelo () e Edivaldo ().

a) Quais as condições de contorno a serem satisfeitas pela onda estacionária formada?

b) Marcelo e Edivaldo movimentam suas extremidades em oposição de fase deslocando-as entre A e -A, de forma a excitar o modo fundamental de oscilação. Qual a função de onda progressiva gerada por Marcelo () e Edivaldo (), se no instante inicial (t = 0) estão segurando a corda nas posições ?

c) Qual a expressão da onda estacionária formada, em função de x e t?

d) Se eles passarem a movimentar a corda em fase, qual a frequência de oscilação mínima excitada? Justifique a resposta.

A figura mostra um instantâneo de três ondas que são produzidas separadamente em uma corda que está esticada ao longo do eixo x e submetida a uma certa tensão T. Quatro elementos da corda estão indicados pelas letras a, b, c e d. Se 1, 2, 3, representa o comprimento de onda da onda i, pode-se dizer que:

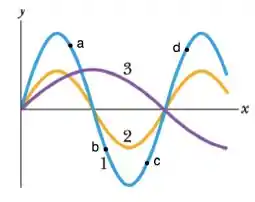
a) . No momento do instantâneo, se a onda 1 se propaga no sentido positivo do eixo x, os elementos a e b da corda estão se movendo no sentido positivo do eixo y e os elementos c e d no sentido negativo.

b) . No momento do instantâneo, se a onda 1 se propaga no sentido negativo do eixo x, os elementos a e b da corda estão se movendo no sentido positivo do eixo y e os elemento c e d no sentido negativo.

c) . No momento do instantâneo, se a onda 1 se propaga no sentido positivo do eixo x, os elementos a e b da corda estão se movendo no sentido positivo do eixo y e os elementos c e d no sentido negativo.

d) . No momento do instantâneo, se a onda 1 se propaga no sentido negativo do eixo x, os elementos a e d da corda estão se movendo no sentido positivo do eixo y e os elementos b e c no sentido positivo.

e) l. No momento do instantâneo, se a onda 1 se propaga no sentido positivo do eixo x, os elementos a e d da corda estão se movendo no sentido negativo do eixo y e os elementos b e c no sentido positivo.

Um sistema para reduzir ruídos sonoros de baixa frequência pode ser instalado em carros e aviões. Seu funcionamento é baseado no princípio de interferência destrutiva, sendo capaz de reduzir (sem eliminar completamente) um som indesejável. Considere que este som indesejável tenha 80 Hz de frequência e nível sonoro de 70 dB e que possa ser representado por uma onda harmônica na forma .

a) Considerando que o sinal gerado pelo aparelho (com mesmo k e que o som indesejado e função de onda ) terá o mesmo sentido de propagação que o som indesejado e emitido da mesma posição, qual a constante de fase do sinal gerado pelo aparelho para que ocorra interferência destrutiva com a do sinal indesejado? Justifique sua resposta.

(b) A partir da intensidade fornecida, determine a amplitude da onda resultante da soma da onda gerada pelo aparelho com a do som indesejável, considerando que o nível sonoro será reduzido para 50 dB. Expresse seu resultado em função de .

(c) Obtenha a função de onda do sinal gerado pelo aparelho e da onda resultante em termos de , k e . Considere que é maior que a amplitude da onda .

Considere o mesmo som indesejado de 80 Hz, mas agora com o sistema redutor em fase com o sinal indesejado mas ligeiramente desregulado, gerando um sinal com amplitude e uma frequência de 84 Hz.

(d) No lugar da interferência destrutiva, que fenômeno ondulatório ocorre neste caso e qual o seu período? Qual é o valor da amplitude máxima resultante?