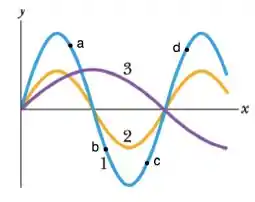
A figura mostra um instantâneo de três ondas que são produzidas separadamente em uma corda que está esticada ao longo do eixo x e submetida a uma certa tensão T. Quatro elementos da corda estão indicados pelas letras a, b, c e d. Se 1, 2, 3, representa o comprimento de onda da onda i, pode-se dizer que:
a) . No momento do instantâneo, se a onda 1 se propaga no sentido positivo do eixo x, os elementos a e b da corda estão se movendo no sentido positivo do eixo y e os elementos c e d no sentido negativo.
b) . No momento do instantâneo, se a onda 1 se propaga no sentido negativo do eixo x, os elementos a e b da corda estão se movendo no sentido positivo do eixo y e os elemento c e d no sentido negativo.
c) . No momento do instantâneo, se a onda 1 se propaga no sentido positivo do eixo x, os elementos a e b da corda estão se movendo no sentido positivo do eixo y e os elementos c e d no sentido negativo.
d) . No momento do instantâneo, se a onda 1 se propaga no sentido negativo do eixo x, os elementos a e d da corda estão se movendo no sentido positivo do eixo y e os elementos b e c no sentido positivo.
e) l. No momento do instantâneo, se a onda 1 se propaga no sentido positivo do eixo x, os elementos a e d da corda estão se movendo no sentido negativo do eixo y e os elementos b e c no sentido positivo.
Passo 1
Do gráfico, nós conseguimos ver que:
E que:
Então:
E:
Show!
Passo 2
Vamos analisar os dois tipos de resposta: onda se movendo pra esquerda e onda se movendo pra direita.
A onda se propaga da esquerda pra direita (sentido positivo do eixo x):
Os pontos a e b estão se movendo pra cima, porque vai passar uma crista por eles.
Os pontos c e d estão se movendo pra baixo, porque vai passar um vale por eles.
A onda se propaga da direita pra esquerda (sentido negativo do eixo x):
Os pontos a e b estão se movendo pra baixo, porque vai passar um vale por eles.
Os pontos c e d estão se movendo pra cima, porque vai passar uma crista por eles.
A única resposta que satisfaz tudo ao mesmo tempo é a A.
Resposta
Letra A.