Um sistema para reduzir ruídos sonoros de baixa frequência pode ser instalado em carros e aviões. Seu funcionamento é baseado no princípio de interferência destrutiva, sendo capaz de reduzir (sem eliminar completamente) um som indesejável. Considere que este som indesejável tenha 80 Hz de frequência e nível sonoro de 70 dB e que possa ser representado por uma onda harmônica na forma .
a) Considerando que o sinal gerado pelo aparelho (com mesmo k e que o som indesejado e função de onda ) terá o mesmo sentido de propagação que o som indesejado e emitido da mesma posição, qual a constante de fase do sinal gerado pelo aparelho para que ocorra interferência destrutiva com a do sinal indesejado? Justifique sua resposta.
(b) A partir da intensidade fornecida, determine a amplitude da onda resultante da soma da onda gerada pelo aparelho com a do som indesejável, considerando que o nível sonoro será reduzido para 50 dB. Expresse seu resultado em função de .
(c) Obtenha a função de onda do sinal gerado pelo aparelho e da onda resultante em termos de , k e . Considere que é maior que a amplitude da onda .
Considere o mesmo som indesejado de 80 Hz, mas agora com o sistema redutor em fase com o sinal indesejado mas ligeiramente desregulado, gerando um sinal com amplitude e uma frequência de 84 Hz.
(d) No lugar da interferência destrutiva, que fenômeno ondulatório ocorre neste caso e qual o seu período? Qual é o valor da amplitude máxima resultante?
Passo 1
a) Antes de começar a fazer essa questão vamos fazer uma oração pra Thor, dar uma esticada, tomar um café e respirar fundo.

Ok, agora podemos.
Vamos chamar o sinal gerado pelo aparelho de:
E o sinal indesejado é:
A fase de cada um é:
Então a diferença de fase vai ser:
Beleza! E pra interferência ser completamente destrutiva, quanto você acha que essa diferença de fase deve ser?
Olha pra essa imagem que eu vou colocar aqui. O que nós queremos que aconteça é isso:
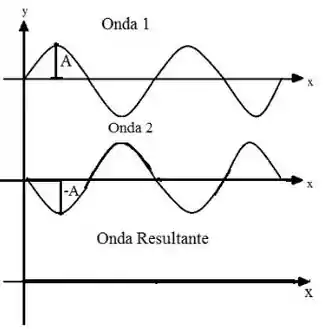
Pra isso acontecer, a diferença de fase entre as ondas deve ser igual a meia volta completa. Como uma volta completa é igual a , a diferença de fase deve ser igual a ! Então:
Passo 2
b) O que você precisa saber neste item é que a intensidade é proporcional ao quadrado da amplitude. Tipo assim:
E esse sinalzinho significa proporcional.
Então o que nós vamos fazer aqui? Vamos achar as intensidades e , porque depois de achar podemos fazer:
E aí podemos dizer com certeza que:
Então agora vamos achar essas intensidades.
Passo 3
O nível sonoro é:
Então:
O valor de foi dado no formulário!
Fazendo continhas de logaritmo, achamos:
Show! Vamos fazer a mesma coisa pra intensidade resultante:
Passo 4
Agora vamos substituir na fórmula lá do início:
Passo 5
c) Ok, agora aqui nós vamos fazer uma parada muito loka.

Acompanha comigo aqui.
Ele quer que a gente ache:
E:
Pra achar só falta né? Porque o resto já temos. Então vamos em busca de .
Vamos usar a fórmula que ele deu no formulário:
Essa fórmula é pra superposição de ondas com mesmo k e mesmo .
Olha que lindo esse produto notável do lado direito:
Como ele disse que só consideremos o caso positivo ao tirar a raiz:
Ok, então:
Passo 6
Agora precisamos achar a onda resultante.
Como já sabemos a amplitude:
E essa fase resultante conseguimos encontrar pela fórmula:
Como e , .
Então:
E:
Passo 7
d) Neste caso temos a superposição de dos ondas de freqüências parecidas, e , no mesmo sentido de propagação e ocorre o fenômeno de batimento. Como as ondas estão em fase e têm a mesma amplitude, porém k e diferentes, podemos escrever (usando o formulário para obter a superposição):
E:
Como a única parte não variável dessa fórmula horrorosa de A(x,t) é , essa será a amplitude máxima.
A frequência de batimento será:
Como o período é o inverso da frequência, o período de batimento será:
Resposta
a)
b)
c) e
d) e