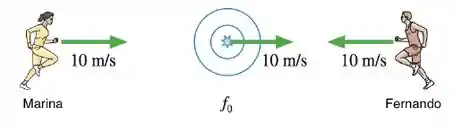
Marina e Fernando se movimentam com velocidades em relação a um observador inercial e estão escutando ondas sonoras produzidas por uma fonte de freqüência que se movimenta com velocidade ⃗ em relação ao mesmo observador, como mostrado na figura. Para as freqüências das ondas sonoras que Marina e Fernando escutam, pode-se dizer:
a) , onde e .
b) , onde e .
c) , onde e .
d) , onde e .
e) , onde e .
Passo 1
Essa questão aí é de efeito Dopler!
A primeira coisa que você tem que perceber é que Marina tá se movendo com a messsssma velocidade que a fonte. Então não vai ter movimento relativo entre elas, não vai ter efeito Dopler aí. Então:
Fernando tá se aproximando da fonte! A fórmula que a gente usa pra Efeito Dopler é:
Esse é a frequência da fonte que é igual a .
E é a frequência percebida pelo observador Fernando.
E esses sinais a gente usa dependendo do referencial, que é sempre positivo no sentido do observador pra fonte. Ou seja, de Fernando pra fonte.
Então , que é a velocidade do observador Fernando, vai ser positiva! Nós vamos usar .
E , que é a velocidade da fonte, vai ser negativa. Vamos usar .
Então:
Como:
Resposta
Letra A.