Marcelo e Edivaldo seguram pelas extremidades uma corda de comprimento L e densidade linear , aplicando uma tensão T. Ao movimentar as extremidades, eles geram ondas harmônicas progressivas em cada extremidade, de forma a obter ao final uma onda estacionária na corda, com os ventres nas posições de Marcelo () e Edivaldo ().
a) Quais as condições de contorno a serem satisfeitas pela onda estacionária formada?
b) Marcelo e Edivaldo movimentam suas extremidades em oposição de fase deslocando-as entre A e -A, de forma a excitar o modo fundamental de oscilação. Qual a função de onda progressiva gerada por Marcelo () e Edivaldo (), se no instante inicial (t = 0) estão segurando a corda nas posições ?
c) Qual a expressão da onda estacionária formada, em função de x e t?
d) Se eles passarem a movimentar a corda em fase, qual a frequência de oscilação mínima excitada? Justifique a resposta.
Passo 1
a) A primeira coisa que você precisa lembrar aqui é que, numa onda estacionária, um ventre tá na mesma posição que uma crista. Então quando ele fala que os ventres estão nas posições de Marcelo e Edvaldo, as cristas também vão estar nessas posições.
As posições de Marcelo e Edvaldo são e . Essas posições serão de máximo (crista) ou mínimo (ventre). Então:
E esse depende se eles estarão defasados ou não. Tipo assim: Marcelo pode tá num vale e Edvaldo numa crista. Nesse caso:
Ou os dois podem estar na mesma posição vertical, de crista ou vale. Nesse caso:
Pegou o raciocínio?

A outra condição de contorno vai ser quanto à inclinação de corda! A derivada da função de onda y(x,t) com relação a x é a inclinação da corda. Nos ventres e cristas essa inclinação é zero, uma reta horizontal! Então nas posições de Marcelo e Edvaldo a derivada com relação a x vai ser zero:
Você não pode esquecer que: essas condições só são válidas pra quando as ondas já se encontraram. Como elas se encontram no meio da corda, , o tempo t deve ser:
Em que:
Então:

Passo 2
b) Então, o que eu te disse no item a: eles poderiam estar em oposição de fase! Ou seja, um tá em +A outro em –A. Show! Além disso, a onda gerada por Marcelo se propaga pra direita (, e a gerada por Edvaldo se propaga pra esquerda (. Então:
Lembrando que as ondas geradas pelos dois tem mesma frequência angular e portanto mesmo k!
Agora, eles tão excitando o modo fundamental de oscilação (aquele em que n = 1). E nós temos fórmulas que relacionam o harmônico às constantes:
Como n = 1:
Show! Guarde essa informação.
Passo 3
Aqui nós vamos usar os dados que ele deu! Que no tempo t = 0: .

Como nós achamos que :
E como (isso aqui é trigonometria, pense no ciclo trigonométrico!):
Para Marcelo:
Então:
Lembrando que:
Passo 4
c) Uma onda estacionária vai se formar quando:
Essa onda vai ser resultado da soma das ondas formadas pos Marcelo e Edvaldo. Ou seja:
Usando a relação :
Só isso!
Passo 5
d) Se as extremidades estiverem oscilando em fase, elas vão ser duas cristas ou dois vales. Pra isso, ainda terão dois nós entre elas. Tipo assim:
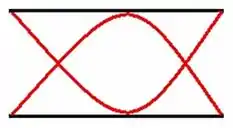
Nesse caso aí, o comprimento de onda vai ser igual ao tamanho da corda:
Dá pra ver isso pela figura, e se você pensar na fórmula, pro segundo harmônico:
Maravilha! E como:
Resposta
a) , e
b) e
c)
d)