PREC de Física 2 da USP - 2013

A energia potencial de uma partícula de massa numa dada posição é descrita pela função (em Joules, sendo em metros), mostrada na figura abaixo.

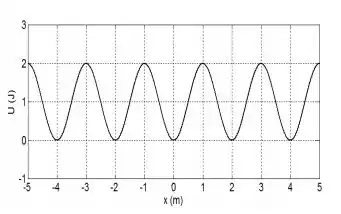
1. Calculo a força que atua na partícula para todo .
2. Calcule a frequência angular de pequenas oscilações em torno de .

Considerando que a partícula é colocada em repouso na posição no instante de tempo e realiza pequenas oscilações em torno de , determine:

3. A posição em função do tempo.
4. A velocidade em função do tempo da partícula, .
5. O módulo da velocidade da partícula quando esta se encontra na posição .

Sugestão: utilize a série de Taylor de em torno de .

Um corpo de massa colide com uma plataforma de massa , inicialmente em repouso e presa a uma mola de constante e massa desprezível (a outra extremidade da mola mantém-se presa a uma parede). No momento da colisão, a mola está relaxada e a velocidade do corpo é . O sistema está imerso em um fluido com constante de amortecimento .

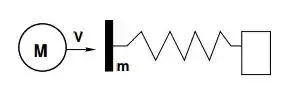
Se a colisão entre o corpo e a plataforma for completamente inelástica, determine:

1. A frequência natural de oscilação do sistema na ausência de amortecimento.
2. O regime de oscilação amortecida.
3. A velocidade do corpo no instante logo após a colisão.
4. A posição do corpo em função do tempo (considere a posição de equilíbrio e o instante logo após a colisão).

A figura ao lado mostra dois gráficos que representam uma onda transversal em uma corda de de massa e de comprimento, descrita por uma função . A onda está se movendo no sentido positivo de . Com base nesses dados e na informação contida nesses gráficos, determine:

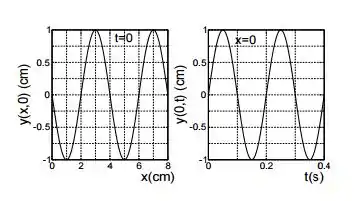
Obs: justifique todas as respostas

1. A amplitude e frequência da onda.
2. O comprimento de onda e a velocidade da onda.
3. A expressão que descreve a onda.
4. A tensão na corda.