A figura ao lado mostra dois gráficos que representam uma onda transversal em uma corda de de massa e de comprimento, descrita por uma função . A onda está se movendo no sentido positivo de . Com base nesses dados e na informação contida nesses gráficos, determine:
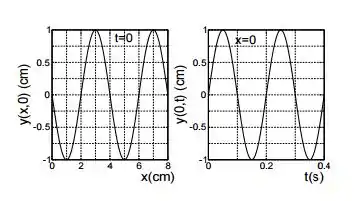
Obs: justifique todas as respostas
- A amplitude e frequência da onda.
- O comprimento de onda e a velocidade da onda.
- A expressão que descreve a onda.
- A tensão na corda.
Passo 1
a):
A onda tem uma fórmula básica assim:
Pelo gráfico, a gente percebe que a amplitude é:
Já que esse é o máximo valor que ele alcança.
Além disso, podemos observar no gráfico da direita que o espaço de tempo que se passa entre dois picos é:
Então, a frequência é:
Ou:
Já que o enunciado não especificou qual frequência( a linear ou a angular) que ele queria.
Passo 2
b):
O gráfico da esquerda mostra que os valores de se repetem a cada . Logo, é esse o valor de :
E como calcular a velocidade?
É só fazer:
Passo 3
c):
Vamos montar a fórmula:
Bom, a gente já calculo
E:
OBS.: repare que a unidade de é . Desta forma, os valores de na nossa expressão para devem ser colocados em .
Já sabemos quase tudo da fórmula, então ele tá assim:
Por que Bom, o enunciado nos deu o sentido da onda. Ela esta seguindo o sentido positivo de , então tem que ser assim, com um menos na frente (:
Então a gente só precisa determinar .
Vamos usar alguns pontos dos gráficos. Pelo gráfico da direita, sabemos que:
Agora vamos usar o gráfico da esquerda. Por ele, sabemos que
Então:
Show?
Então:
Passo 4
d):
Ai a gente tem que usar:
A gente já calculou , mas quanto vale a densidade linear
Bom, a densidade linear, por definição, é:
Como sabemos a massa da corda e o seu comprimento:
Como estamos usando unidades com , precisamos passar a nossa velocidade pra
Então:
Resposta
a):
b):
c):
d):