Um corpo de massa colide com uma plataforma de massa , inicialmente em repouso e presa a uma mola de constante e massa desprezível (a outra extremidade da mola mantém-se presa a uma parede). No momento da colisão, a mola está relaxada e a velocidade do corpo é . O sistema está imerso em um fluido com constante de amortecimento .
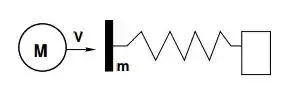
Se a colisão entre o corpo e a plataforma for completamente inelástica, determine:
- A frequência natural de oscilação do sistema na ausência de amortecimento.
- O regime de oscilação amortecida.
- A velocidade do corpo no instante logo após a colisão.
- A posição do corpo em função do tempo (considere a posição de equilíbrio e o instante logo após a colisão).
Passo 1
a):
Como o corpo vai colar na mola, eles vão passar a ser um corpo só. Assim, a frequência natural pode ser calculada como:
E a massa total é:
Então:
Passo 2
b):
Aqui ele tá querendo saber se o regime é crítico, subcrítico ou supercrítico. Uma boa forma é comparar com
O enunciado te deu e a massa total. Pra calcular
Como:
A gente conclui que esse regime é o crítico.
Passo 3
c):
Bom, aqui a gente precisa lembrar daquele conceito de mecânica: conservação de momento.
Já que é uma colisão, o momento se conserva, e como é uma colisão totalmente inelástica, os corpos permanecem juntos ao fim da colisão. Podemos calcular assim:
Passo 4
d):
A solução geral para o caso critico é assim:
Vamos às condições inicias:
Então:
Resposta
a):
b):
Crítico
c):
d):